Sheaf is an important subject in mathematics and there are many ways to approach the subject, here we look at the category theoretical aspects otherwise see:
- from open sets of a topological space.
- from a generalisation of the concept of a fibre bundle.
Presheaf
A 'presheaf' category is a special case of a functor category (see page here). It is a contravarient functor from a category 'C' to Set.
Since it is contravarient it is usually written:
Cop->Set
or
SetCop
There is more about presheaves on the page here.
Example - Fibre Bundle as Endo Function
| C |  |
Every element has 1 outgoing arrow. May have zero or multiple incoming arrows. |
| Cop |  |
Every element has 1 incoming arrow. May have zero or multiple outgoing arrows. |
| Cop->set |  |
Every element maps to a set. |
This page explains Fibre bundles.
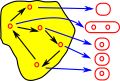
Presheaf Example - Single Element SetA very simple example would be where Cop is a single element set (terminal object in set). Hom( Cop, Set) therefore contains set of single arrows, one for every element of the set. |
 |
Presheaf Example - GraphSee this page. |
 |
Presheaf Example - Relational DatabaseSee this page. |
 |
Sheaf
We can think of a sheaf as building a more complicated structure from simpler components. These simpler components come from the presheaf.
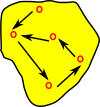
To investigate this take the graph example from above. We can take individual edges and glue them together to form a more complidated shape.
| An individual edge is defined by its source and target verticies. So this diagram must commute. |  |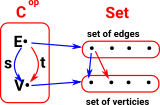
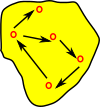
| Multiple edges can be glued together. Here the source of one edge is connected to the target of another edge. Note, although the definitions in Cop are the same the squares don't all commute unless we keep them separate. |  |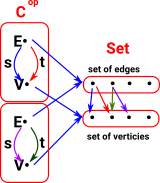
Generalisation of a Fibre BundleThis is discussed from a topological point of view: For example, where there is a family of types indexed by elements of another type.
|
 |
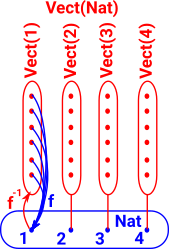| The type families in fibre bundles are disjoint. One way to extend that concept is to allow an overlapping type family. |  |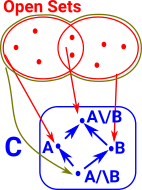
Sheaf - Tracking Locally Defined Data
A sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space.
Sheaves, with mappings which preserve this open set structure, form a category. This open set structure can be extended to groups, abelian groups, or commutative rings. To make it more general and apply it to more general categories we use the concept of presheaf which uses 'restriction morphisms'. More about presheaf on page here. |
 |
