Chain Complexes

This page follows on from the discussion of delta complexes here. We now want to represent this topology in algebra terms.

We start by defining two functions on δ (functions from a function to a subset) which define subsets of the codomain and domain respectivly:

• Boundary: boundary at n given by Im δ_n+1
• Cycle: cycle at n given by Ker δ_n

where:

• Im is the image of δ which is the subset of a function's codomain which is the output of the function on a subset of its domain.
• Ker is the kernel of δ which is the subset of the domain which maps to zero. (gives partition of the domain that expresses equivalence).

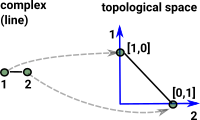
Example 1 : Circle

A circle (not filled in) is topologically equivalent to an empty triangle.

So our faces are: points: a, b and c edges: ab, -ac and bc

We can calculate cycles and boundaries as follows:

Boundary

We can now relate them using the boundary function. This boundary function removes each element in turn and alternates the sign.

B₀ = Im δ₁ = a-b, a-c, b-c

• δab = a-b
• δac = a-c
• δbc = b-c

So the boundary of the edges is the verticies.

B₁ = Im δ₂ = 0

The boundary of 0 is 0.

Higher order boundaries are all zero.

Cycles

The cycles are given by the 'kernel' of δ_n which are the 'chains' which map to zero

Z₀ = Ker δ₀ = a,b,c

This is given by the kernel of δ₀ which are the vertices which map to zero, and they all map to zero because δ₀ maps everything to zero.

Z₁ = Ker δ₁ = ab->bc->ca , bc->ca->ab , ca->ab->bc

We want the kernel of δ₁ which are the edges which map to zero, here 'zero' can be interpreted as the identity mapping (a mapping from an element back to itself). So the cycles are the loops around the circle starting at any vertex and ending on that vertex.

Z₂ = Ker δ₂ =

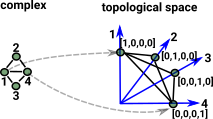
Example 2 : Disk

A disk (filled in circle) is topologically equivalent to a solid triangle.

So our faces are: points: a, b and c edges: ab, -ac and bc triangle: abc

We can now relate them using the boundary function:

• δabc = ab -ac + bc
• δab = a-b
• -δac = c-a
• δbc = b-c

This boundary function removes each element in turn and alternates the sign.

So if we apply boundary twice we get:

δ(δabc) = δ(ab -ac + bc)
= (a-b) + (c-a) + (b-c)
= 0

So, in this case, applying boundary twice gives zero.

In fact applying delta twice always gives zero: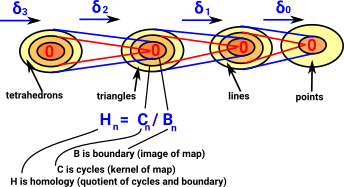

Chains

In the earlier examples we just looked at the delta operator on single triangles. Here we look at a chain of triangles: This gives the boundary of the shape.

As a Free Abelian Group

Now we allow integer multiples and sums of these. If i,jk... are integers then we have:

δ( i ab - j ac + k bc) = i (a-b) - j (a-c) + k (b-c)
= (i-j) a + (k-i) b + (j-k) c

This gives a free abelian group isomorphic to Z.

Chain Complex as a Sequence of Abelian Groups or Modules

C0	Zero dimensional chain = free abelian group on vertices. Elements of C0 are intergral linear combinations of vertices such as: 2x+7y+5z
C1	One dimensional chain = free abelian group on directed edges. Elements of C1 are intergral linear combinations of edges such as: 2xy+7xz+5yz These don't necessarily need to be a cycle.

We now treat δ as a group homomorphism which extends *.

δ(C₁)->C₀

Being a group homomorphism means respecting the group structure of the two groups, that is,

• δ(u+v) = δ u + δ v
• δ(u^-1) =(δ u)^-1

It also respects the extra structure that groups are required to be continuous.

Algebraic meaning of cycle: δ(X) = 0

We find cycles by finding null space of augmented matrix.

Co-Chain Complex

The difference between co-chain complex and a chain complex is that, in a co-chain complex the boundary operator increases the dimension rather than decreases it.

Next Steps

For information about how this can be implemented in computer code here.

Or to continue on the theoretical route see how this is used in homolgy here.

EuclideanSpace

home

Where Are You

This is one of a series of pages about topology, these pages start here.

For other pages, on the site, about topology see:

• Open Sets
• Fibre bundles
• Simplectical Complexes
• Delta Complexes
• Homotopy
• Homology

Computer Code Implementation

I have written some code to implement algebraic topology structures. This is described on the page here and the actual code is on GitHub here.

Topological Space and Simplicial Sets (Geometric Realisation)

Topological spaces have some nice properties, they have the concept of nearness in the most general way. However topological spaces have some quite stringent requirements, geometric realisation gives use a way to embed any CW complexes or simplicial set as a topological space.

A first thought for how to embed simplicial sets in topological spaces might be to equate each simplex with an open set, unfortunately this won't work for the following reasons: Every union of simplices in a CW complex is not a simplex but unions of open sets must be open sets. Every pair of simplices don't necessarily have an intersection.

There is a way to canonically get a topological space from a simplicial complex, this requires a much higher dimensional space so its not very intuitive. For instance, to encode a graph (2D complex), each vertex in the graph needs to have its own dimension in the topological space.

Here we want to encode a complex with two points and a line. We embed this in 2 dimensional Euclidean space (and therefore topological space). Each of the points is now a vector in its own dimension, these are [1,0] and [0,1] and they are the basis vectors. The line is a straight line between these basis vectors, parameterised by t like this { (1-t)*[1,0]+t*[0,1] | t[0,1] }.

A more complex graph gives a lot more dimensions which makes visualising the topological space harder.

For more information about geometric realisation see the page here.