Maths - Topology - Martin Baker

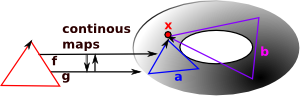
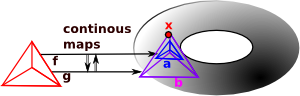
Here we are concerned with shapes, when they are the same shape and the mappings between them.

For example, continuous mappings as allow a toroid to be continuously mapped into a mug.

It is like a sort of 'rubber geometry' where there are no absolute distances.

Determining Same Shape

There are different ways to 'equate' shapes such as homotopy equivalence and homeomorphisms.

We can use 'invariants': properties of topological objects which do not change under certain mappings.

are they split into multiple parts?
number of holes
homology group
homotopy group

Often we need to know if a shape can be continuously deformed into another shape. There are different types of continuous maps.

For instance a Möbius band is homotopy equivalent to a non-twisted band but they are not homeomorphic.

Homeomorphism

A homeomorphism is quite a strict form of 'same shape'. There is a 1:1 correspondence between points on the two shapes. A point is mapped to a point on the other shape and the mapping in the reverse direction takes it back to the original point.

This is like an isomorphism with continuous mappings.

As these are continuous mappings, points that are near to each other must be mapped to points that are also near to each other.

The concepts of nearness and continuous mappings are defined more fully on the page here.

Homotopy Equivalence

A homotopy equivalence is a looser form of 'same shape' than a homeomorphism.

There are continuous maps that are not allowed in a homeomorphism. For example, a line can be continuously contracted down to a point but that would not be allowed in a homeomorphism because the reverse mapping would not take every point back to itself.

Therefore a homotopy equivalence is commonly used rather than a homeomorphism.

This allows more shapes to be considered the same. For example a Möbius band can be continuously deformed to a non-twisted band by first contracting it continuously to a circle and then continuously expanding it to a band.

diagram

How this can homotopy equivalence be defined more precisely?

We can't map every point in X to a point in Y and require an inverse map which brings the point back to where it started.

Continuity

So we need a way to make this continuity idea more precise.

Continuous Maps

A function is continuous if it doesn't jump, that is, when two inputs of the function get close to each other then the corresponding outputs of the function get close to each other.

Here we discuss the most general form of continuous map which also applies to non-metric topological spaces.

A continuous mapping implies a limited kind of reversibility, at least locally.

Definition 1

Here is one definition of continuity, based on open sets:

Let X and Y be topological spaces. A function f : X->Y is continuous if f^-1(V) is open for every open set V in Y.

Definition 2

Another definition of continuity, based on neighbourhoods, is equivalent to the above definition.

Let X and Y be topological spaces. A function f : X->Y is continuous if for every x

X and every open set U containing f(x), there exists a neighbourhood V of x such that f(V)

More detail about continuity on page here.

Continuous Surjective Maps

Here is an extreme case of a Surjective Map which maps to a single point.

This seems to meet the requirements as there is an open set round the whole preimage. We can think of surjections which meet these requirements as 'nice surjections'.

See fibrations

Continuous Injective Maps

Here is an extreme case of a Injective Map which maps from a single point.

In this case all the open sets in the codomain need to map back to a single open set in the domain. This meets the requirements so it is a 'nice injection'.

See cofibrations

Fibration - Line to Point Map Example

To keep things simple, take the example of a line continuously retracted down to a point.

To see this, in its most general form, as a continuous map between topological spaces I have drawn the line consisting of representative points and open sets.

For it to be a continuous map the preimage of an open set must be an open set.

We don't want to have to make any arbitrary decisions about which open set to map back to, so the preimage is the open set around the whole line.

The red arrow is a map between open sets.

This is the homotopy lifting property. When we look at more complicated examples (see fibration page) we will see structure between points being lifted to structure between open sets.

(Co)fibration - Point to Line Map Example

In a homotopy equivalence (but not a homeomorphism) we can have continuous maps between a line and a point.

For the direction from the line to the point all the points in the line map to the point A.

For it to be a continuous map the preimage of the open sets must be an open set. So the open set containing the point maps to an open set around the whole line.

For the direction from the point to the line a map f: A -> Y can only map to a single point in the line.

In order to map to the whole line we need a whole family of maps h: A×[0,1] -> Y

That is a homotopy, there is a continuous mapping between the maps.

For it to be a continuous map the preimage of the open sets must be an open set. So all the open sets in the line must map back to the open set containing the point.

This is the homotopy extension property. When we look at more complicated examples (see cofibration page) we will see a mapping to a subset can be extended to the whole set.

Homotopy Equivalence

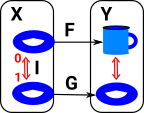
If we continuously map every point in X to a point in Y and require an inverse map which brings the point back to where it started and do this in both directions we get a homeomorphism.

But if we want a homotopy equivalence (shapes which can be continuously deformed into each other) then we only need a weaker requirement that this round trip and the identity maps are a homotopy.

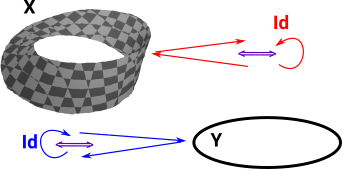More about homotopy equivalence on the page here.

Homotopy

For comparison start with the idea of functional equality:

if F(x)=G(x) for all x
then F=G

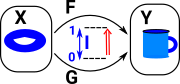We need a weaker form of sameness to allow, say, a torus to be somehow the same shape as a cup.

Here the points F(x) and G(x) are different but both functions still cover the whole cup.

Homotopy

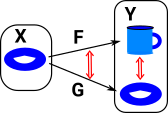If we have two topological spaces X & Y with two continuous maps between them F & G then a homotopy is a continuous map between F & G.

In order to see how this is related to the map between the cup and torus I have drawn a map from a third shape (in this case another torus).

So as F continuously maps the G then the cup maps to the torus.

We can move the continuous map forward from the functions to the domain so the functions are homotopic if:

H: X × [0,1] -> Y

where:

H(x,0) = F(x)
H(x,1) = G(x)

We can think of this as 'filling in' the gap between F and G so that we can take any path through it.

Or we can draw it in the codomain (currying) so that each element in X maps to I->Y.

More about homotopy on page here.

In two dimensions it is relatively easy to determine if two spaces are topologically equivalent. We can check if they:

are connected in the same way.
have the same number of holes.

However, when we scale up to higher dimensions this does not work and it can become impossible to determine homeomorphism. There are methods which will, at least, allow us to prove more formally when topological objects are not homeomorphic.

These methods use 'invariants': properties of topological objects which do not change when going through a homeomorphism. Here we look at two types of invariants which arise from homotopy and homology.

Homotopy

It would take up too much space to properly explain the concept here so see this page for more details

nth homotopy group

If 2 spaces are homotopy equivalent the fundamental groups are isomorphic.

In homotopy we use equivalence classes between a circle and loops (which don't collapse) on the topological object that we are investigating. We can get further invariants by extending the circle to the surface of higher order n-spheres.

We can then get algebraic structures (mostly groups) by investigating what happens when these loops are composed, the loops are generators of the group. In homotopy the order of these compositions can be significant, that is the groups are not necessarily abelian.

Homology

It would take up too much space to properly explain the concept here so see this page for more details

homology groups

In homology we don't just use n-spheres but every closed oriented n-dimensional sub-manifold.

It also uses a different definition of equivalence classes where composition of loops commutes. This results in abelian groups.

So we don't need to fix the basepoint.

Example

Are the two shapes on the right 'homotopy equivalent' ?

Is there a continuous map between them in both directions?

There is more about this example on the page here.

Topology on a Set

A topology on a set X is a collection Τ of subsets of X, called open sets satisfying the following properties:

X and Ø are elements of Τ.
Τ is closed under finite intersections.
Τ is closed under arbitrary unions.

The requirements for the existence of of meets and joins correspond to the requirements for the existence of unions and intersections of open sets. Therefore these lattice structures can represent topologies.

	Lattice	Open Set



invalid - every intersection should be an open set:

Venn Diagram	Topological Space (or not)	Lattice (frame)
	This is not a topological space because 'a' and 'b' are subsets but not the union of 'a' and 'b'
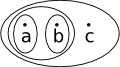	This is now a topological space because we have added the union of 'a' and 'b'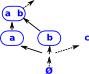
	This is not a topological space because 'ab' and 'bc' are subsets but not their intersection.
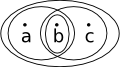	This is now a topological space because we have added 'b'

Note: Assume Ø is included in the above examples.

Topological Space

In many cases the concept of a metric space is unnecessary, however we still need the concept of 'nearness' and hence 'continuity'. 'Topological space' based on the 'topological open set' is the most general way we can do this. This allows us to define nearness purely using the concept of a subset.

Hausdorff Space

Hausdorff space is a bit more specific than general topological space. Space is Hausdorff if, in addition to being a topological open set, for any two points:
x₁, x₂X there are disjoint open sets U₁, U₂ that contain x₁and x₂.

Basis

A basis is a subcollection B= U

where

U is the open set
B is the basis
= a subcollection (subset) - I need to add the proper symbol for this.

such that every element of U is a union of open sets in B.

Link between Topology and Logic

One way to visualise the link between topology and logic is to start with a Venn diagram.

We can then map points in the Venn diagram to either true or false depending on whether they are in a given set.

Maths - Algebraic Topology

Determining Same Shape

Homeomorphism

Homotopy Equivalence

Continuity

Continuous Maps

Definition 1

Definition 2

Continuous Surjective Maps

Continuous Injective Maps

Fibration - Line to Point Map Example

(Co)fibration - Point to Line Map Example

Homotopy Equivalence

Homotopy

Homotopy

Homotopy

Homology

Example

Topology on a Set

Topological Space

Hausdorff Space

Basis

Link between Topology and Logic

Link between Topology and Category Theory

Presheaf

Fibre in Category Theory

Slice Category

Examples

Non-Geometric Examples

Sequences

Denotional Semantics

Recursively Defined Structures

Further Information

EuclideanSpace

Where are you

Related Subjects

Other Subjects

Homology

Inverse Functions