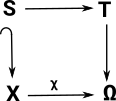
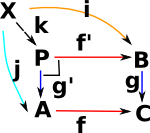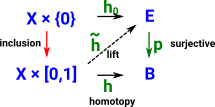| Given fixed objects A,B,C and morphisms g,f then a pullback is P with some universal property. |  |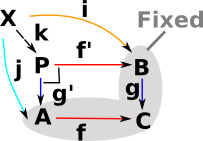
Pullback is a:
- Generalisation of both intersection an inverse.
- If a category has binary products and equalizers, then it has pullbacks.
In programming terms it is related to the concept of indexing.
The pullback is like a type of division for function composition, in other words if multiplication is function composition then what is division? This comes in left and right flavors that is:
if h = g o f
- We know f and h, how do we find g?
- We know g and h, how do we find f?
Example in Set
Pullbacks add some extra structure to products (see page here). This can allow us to restrict to certain arrows and make other paths commute.
 |
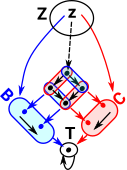
Here we take a product in set (as described on page here) and add another object T. This forms a square which must commute. As a starting point the new object T is the terminal object. So everything maps to it and so the square commutes. This is a pullback, but in a trivial way, because it does not add any restrictions to a product. |
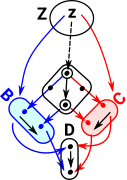
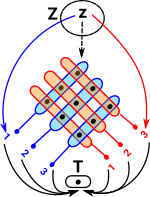
Now replace T with a two element set D which has elements a and b. The requirement for the square to commute means that some elements in the array are no longer used. So we can think of the pullback as restricting the elements of the product. |
 |
 |
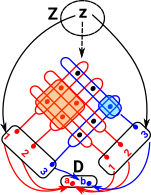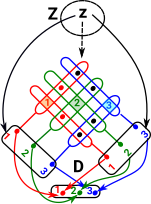At the other extreme from the terminal object case, here we have a 1:1 correspondence between the elements of D and the rows and columns of the product. This restricts the array to its leading diagonal so the projections are 1:1 (or at least monomorphisms). This concept can be extended from sets to pullbacks in other categories. Pullbacks preserve monomorphisms and isomorphisms: ncatlab. |
Set Example 1
 |
This diagram is both a pullback and a pushout. |
 |
Set Example 2
How does the above example relate to the idea that the pullback is a subset of the cartesian product of two sets? We have this restriction on the Cartesian product:
Σ<a,b>
A×B| f(a)=g(b)
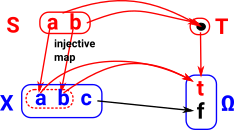
| So, in this example, 'P' contains only the subset of the Cartesian product shown in red (that is <e,e>). |  |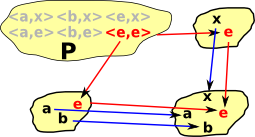
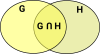
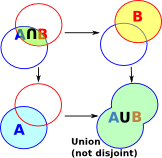
Pullback and Intersection
The above case suggests that, in the most general case, injective maps don't work for the projections. However, if we impose a limitation by making the product a pullback, then it works and the 'product' can be an intersection.
see ncatlab
Pullbacks in other Objects
In sets the product contains an array of ordered pairs, in more general objects these may not all exist.
For product topological spaces, products are taken at the level of the underlying sets and endowing them with an initial lift structure, the smallest or initial topology for which the projection maps are continuous. see ncatlab
A partially ordered set can be treated as a category, using the order relation as the morphisms. In this case the products and coproducts correspond to greatest lower bounds (meets) and least upper bounds (joins). see wiki.
Pullbacks in Directed Graphs
We looked at this example for catagorical products on page here. Here we extend the example to pullbacks of two directed graphs.
 |
The simplest way to convert the product to a pullback is to add maps from B and C to the terminal obgect. This does not add any restrictions to the product so we still have a Cartesian product. In a Cartesian product there is an arrow from (g,h) to (g',h') iff:
|
We can take the opposite extreem. Here there is an element in D for every element in B or C. This gives a tensor product. In a tensor product there is an arrow from (g,h) to (g',h') iff:
|
 |
This is a similar construct to a fibration (see page here) but here we have not invoked the concepts of a topological space or continuous maps between them.
In general for graphs:
- Pullbacks always exist.
- Pushouts do not necessarily exist
Table of Results
| Pullbacks | Pushout | |
|---|---|---|
| universal cone over diagram |
|
|
P is the pullback of f along g or g along f (A,B,C fixed) . Square must commute (in best possible way) so any other square, also containing (A,B,C) must uniquely map to it. |
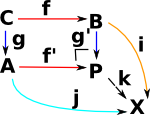
P is the pushout of A,B,C |
|
| generalisation |
|
a kind of colimit |
| examples: set: | Σ<a,b> where: k(x) maps to <j(x),i(x)> called a fibred product. |
A U B /equivalence relation |
In Graphs |
Pullbacks always exist. | Pushouts do not necessarily exist. |
In concrete categories the Cartesian product is often the categorical product. The pullback is like the categorical product but with additional conditions. So in the following examples we have a Cartesian product with a subset of the rows and columns.
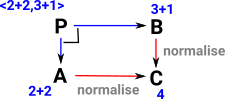
Example in Number ExpressionsThis generates pairs of elements <a, b> : P with a in A, b in B, such that f(a) = g(b). So the requirement for this square to commute generates in P all the possible pairs of numbers that are equal to each other. So, in the example on the right, 4 is a 'representative' for all the things it is equal to such as 2+2 and 3+1. Sometimes the notation [4] is used for the set of all the things it is equal to (although this notation could be confused with list). More about this on Leibniz equality page. |
 |
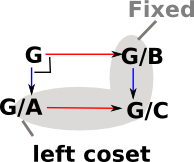
Examples in Groups
 |
Substitution as Pullback
Can we express substitution in category theory terms? See discussion on page here.
| Substitution of a term into a predicate is pullback, but substitution of a term into a term is composition. | |
| Type theory version | Substitution of a term into a dependant type is pullback, but substitution of a term into a term is composition. |
There is a discussion of this topic on this site.
Say we have two propositions, say:
- y = 2*x+1
- z = w + 3
Then, under certain conditions, we could substitute a variable for a term. Say, let w=y so:
- z = (2*x+1) + 3
 |
So here we draw this substitution as a pullback.
|
Pullback as Generalisation of Inverse
Hence we have two morphisms to C so this looks like the given part of a pullback. |
 |
 |
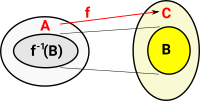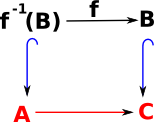To complete the square we add cone for this diagram and we call it f-1(B) to emphasise that it is the inverse of 'f'. |
Reversing a function can generate interesting structure, for example, reversing addition on natural numbers leads to the integers and reversing multiplication leads to fractional numbers.
| If we reverse a surjective mapping, where many elements in the domain map to a single element in the codomain, then reversing the function gives a fibre bundle. |  |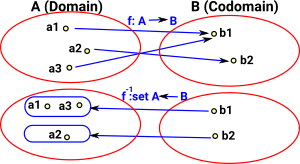
| If we reverse a injective mapping, where not all elements in the codomain are mapped to, then reversing the function gives a subobject structure. |  |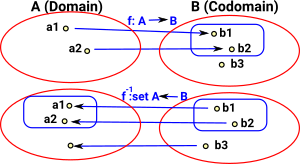
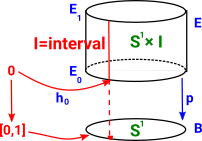
Continuity as Pullback
This diagram shows a set of points being mapped to another set of points (in red). For that map to be continuous the pre-image of every open set must be an open set (shown as blue map in the reverse direction). |
 |
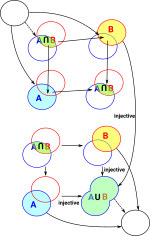
Pullback Properties of Injective and Surjective Maps
|
 |
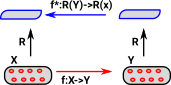This can be proved from:
- f is injective if and only if it has a left inverse
- f is surjective if and only if it has a right inverse
(pulling back swaps left and right)
Let f:X->Y and g:Y->X.
if g•f=id.
- g is a left inverse to f
- f is a right inverse to g
if f •g=id.
- f is a left inverse to g
- g is a right inverse to f
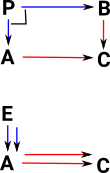
Relationship to Equaliser
If the category A is the same as the category B then the pullback becomes an equaliser. See equalisers on this page. |
 |
Related Pages
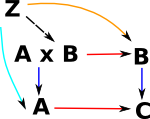
Examples in Various Categories
| Product (pullback) |
||
|---|---|---|
 |
||
| generalisation | a kind of limit | |
| set example |  |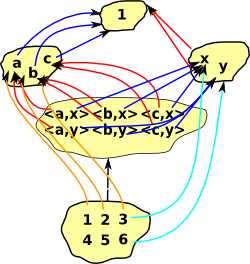
cartesian product {a,b,c}*{x,y}= |
| group | the product is given by the cartesian product with multiplication defined component wise. | |
| Grp (abelian) | direct sum | |
| vector space | direct sum | |
| poset | greatest lower bound meet |
|
| base topological space | ||
| POS | greatest lower bounds (meets) |
|
| Rng | ||
| Top | the space whose underlying set is the cartesian product and which carries the product topology | |
In Graphs |
Pullbacks always exist. (Pushouts do not necessarily exist.) |
|
| category | objects: (a,b) morphism: (a,b)->(a',b') |
tensor products are not categorial products.
In the category of pointed spaces, fundamental in homotopy theory, the coproduct is the wedge sum (which amounts to joining a collection of spaces with base points at a common base point).
