Or Fiber (alternative American spelling).
Fibration captures the idea of one category indexed over another category. It does this in a categorical way, that is, defined in terms of arrows.
A fibre is a more general (weaker form) of:
- a projection
- a pullback or pushout (fiber (co)product) - indexed and indexing category are the same.
- a comma category.
- one quantity defined 'over' another such as a field space.
- a base space.
- sorting or partitioning.
Example in Set
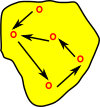
If we take a mapping from A to B (in this case surjective) We might think of this as partitioning or indexing A into disjoint subsets but there is no unique arrow going the other direction (from B to A). |
 |
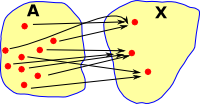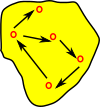
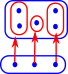
We can put the elements into subsets, that is, if A was a set then change it to a set of sets. I have changed the name of 'B' to 'I' because we want to think of it as an indexing set. |
 |
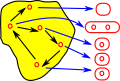
| Since we have put the elements into subsets we can reverse the arrows. |  |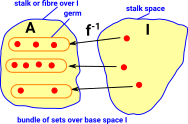
We can define the sets in A in terms of the inverse mapping.
Example - Fibre Bundle as Endo Function
| C |  |
Every element has 1 outgoing arrow. May have zero or multiple incoming arrows. |
| Cop |  |
Every element has 1 incoming arrow. May have zero or multiple outgoing arrows. |
| Cop->set |  |
Every element maps to a set. |
This page explains Fibre bundles.
Generalising to Categories
To generalise the idea of getting a fibre structure by reversing the arrow we can change an arrow into the category to an arrow out of the opposite category. The 'presheaf' category is discussed on this page. |
 |
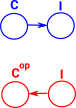Category of bundles over 'I'
We can turn this around and start with 'I', We can then construct a whole category of bundles that could map to it.
| Construct in Bn(I) | Corresponding construct in set |
|---|---|
Bn(I)= |
Set I |
| category of bundles over I | the comma category of functions with codomain I |
| pullback object (P,j) | bundle of pullbacks from set |
| subobject classifier | bundle of two element sets |
| Sections | |
| Products | |
| Exponentials |
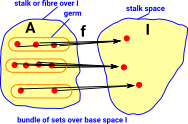
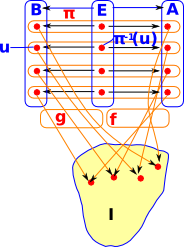
In Bn(I) objects are pairs, consisting of an object and a map from that object to I. Represented as: (A,f) where f:A->I
If we have multiple bundles over I then, we can define morphisms in the category, so that this diagram commutes. See comma category on this page. |
 |
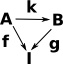| In terms of its internal objects: |
Here we add another stalk 'B' and add a morphism: In order for the diagram to commute then the internal arrows can only go from an element in a germ in 'A' to an element in the corresponding germ in 'B'. |
 |
|
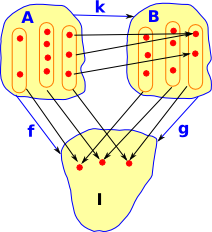We could re-draw this as a set of fibres, within a bigger fibre, indexed by I. The inner fibre can be permutated and the outer fibre can be permutated but the inner strands can't be moved between outer fibres. |
 |
|
 |
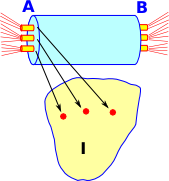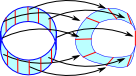So if we take the example of the Möbius band, that we looked at on the page here, we can see it as a fibre. It is arbitrary where it starts and ends so it is only where we take the local view that we see it as two fibres. |
 |
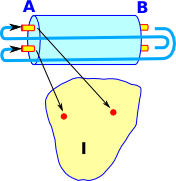Preservation of Product
A projection along a fibre looks, locally but not necessarily globally, like a product space. The diagram on the right is intended to show a non-linear space but locally it is still a product (The contours cross at right angles). This can be represented by a pullback square, as discussed on the page here. |
 |
 |
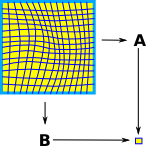Fibre Bundle
 |
π is a 'continuous surjective map' that behaves locally like B×F->B. |  |
Terminology
The terminology is somewhat 'Botanical' suggesting fibres growing out of I:
In geometric terms: I is a base space and A is a projection. |
 |
Fibrations of Graphs
theory: topological graph theory
| undirected graph: | covering projection |
| directed graph: | fibration (weaker form of covering projection) |
Here is an example for directed multigraphs. Each node in the top graph maps to the bottom graph (fibration). The corresponding node always has the same number and colour of incoming arcs (but not necessarily outgoing arcs). This gives some sort of local invariance. |
 |
| We can make a mapping between these graphs. |  |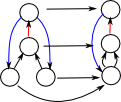
| We can't reverse the mapping completely because we can't have one-to-many in a function but we can map to sets. This gives a fibre bundle. |  |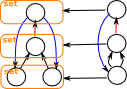
Types
Here we look at applications of fibre bundles to type theory (discussed on page here).
| Here we look at a type, not like a set as a membership relationship, but more like a projection. So if we know that something is 1 or 2 then that tells us something about it, if we know that something is a number then that still gives us information about it but less than if we knew its value. |  |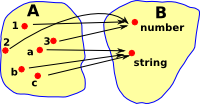
Dependent Types
The situation where a type depends on the value of another type (called a dependent type) is modeled by fibre bundles. So a model of a vector category depends on its dimension: |
 |
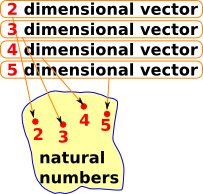Fibre Concept In Topology
In topology the concept of 'nearness' can be defined in a looser way than metric spaces, this is done by using 'open sets' as described here.
A fiber is such a topological space which is parameterized by another (called a base).
- Fiber bundle - map between fibres in the same space.
- Fibration - fibers need not be the same space
Fibrations do not necessarily have the local Cartesian product structure that defines the more restricted fiber bundle case, but something weaker that still allows 'sideways' movement from fiber to fiber.
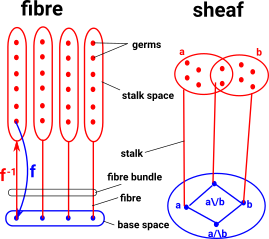
Sheaf
A sheaf can be thought of as a generalisation of a fibre - more on this page.
Enriched Category
No unique functor between objects but multiple functors (hom-set).
Allows us to represent a metric space as a category.
Fibrations
| Relationship between fibrations |  |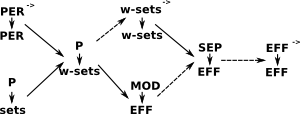
Where:
- EFF = effective topos
- PER = Partial Equivalence relations (symmetric and transitive but not necessarily reflexive) .
- SEP= Section Extension Property.
- w-sets =
From B.Jacobs 'Categorical Logic and Type Theory' p33 w-set |
w-set is a set together with, for each element x E = existence predicate of the w-set |
From Wikipedia PER |
In type theory, constructive mathematics and their applications to computer science, constructing analogues of subsets is often problematic in these contexts PERs are therefore more commonly used, particularly to define setoids, sometimes called partial setoids. Forming a partial setoid from a type and a PER is analogous to forming subsets and quotients in classical set-theoretic mathematics. |
| From Dold | Fibrewise X space over B has the SEP (Section Extension Property) if for each subset B' of B ever section of X over B' can be extended to a section of X over B. |
X, a non-empty set of natural numbers written as: E(x)
NatFibrewise Space
https://www.amazon.com/Fibrewise-Homotopy-Springer-Monographs-Mathematics-ebook/dp/B000W7YA48/
As a Pullback
See pullback page.
