A dependent type is modeled mathematically as a fibre bundle. We discuss fibre bundles in topology context on the page here and in the category theory context on the page here.
The theory of fibres is conventionally explained in terms of sets but here we are working with types. There is a fundamental difference between a set and a type which is that the elements (terms) of a type don't exist outside that type. This makes working with the concept of subtype more problematic.
One of the ways of describing dependent types (on the page here) is as a type indexed over a set. The theory of fibres gives us a way to generalise this set to a more general type.
So, as an example, a vector depends on its dimension: |
 |
| In set theory each element of set A corresponds to a set but, on this page, we are concerned with types, so in this diagram B (Base) and En are types. | 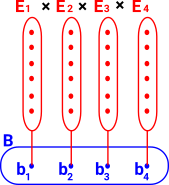 |
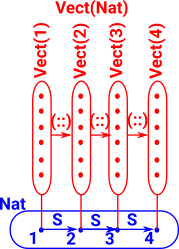 |
Fibre Product
We can take the product of these fibres so we have two bases (indexes - in the diagram B and C) over the same space. An example might be matrices as a vector of vectors. This change of indexes is related to the concept of substitution. More information about fibre product as pullback on this page. |
 |
Fibre
A fibre is a generalisation of a fibre bundle where the elements of the base space don't have to be members of the same type.
An example is one type defined 'over' another type. We can again use vectors as an example where we could have vectors over reals or vectors over complex numbers. |
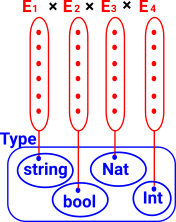 |
Geometric Example
Shown is a common example where a spiral projects onto a circle. To reverse the direction of this projection we have to create a set (type) of points. In this example of a spiral, it can be projected onto a circle since any local section corresponds to a section of a circle. Locally a section of the spiral looks like a section of the circle, globaly the circle and the spiral are different. |
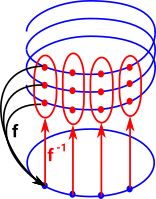 |