We sometimes think of an algebra as a set plus some form of 'structure' (in a similar way that in the computer programming world we look at objects as data+functions) on these pages we look at this structure element of mathematical entities like algebras.
This structure may be defined in terms of:
- Functions such as Binary (or unary or 'n'ary) operations: (element,element) -> element
- Binary (or unary or 'n'ary) relations: (element,element) -> boolean
- mappings (or morphisms or arrows) between objects.
On this page we look at maps or morphisms between objects.
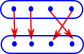
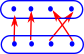
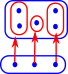
On this page we look at graphs.
Structures with binary operation and identity element
A common type of structure is one with a binary operation and identity element. These structures may have:
- Single objects or multiple objects
- Composition law or not.
- Invertible or not.
As indicated in the following table:
| single objects | multiple objects -> | |||
| composition law | no composition law | |||
| invertible | (permutation) Groups |
all morphisms are isomorphisms |
Graph | |
| non-invertible | Monoids | Categories | Directed Graph |
These structures can all be represented by directed graphs with various restrictions. For instance,
- An invertible structure wont have an arrow from 'a' to 'b' unless there is also an arrow from 'b' to 'a'. (symmetry)
- A structure with composition law, if it has arrows a->b and b->c, then it also has an arrow a->c
- A structure with reflexive law always has identity element, arrow from 'a' to 'a'.
Note: the above bullets correspond to equivalence relations.
Set + Structure
In its purest form the only information contained in a set is the number of elements it contains. All other information, such as labeling the elements, can be added using functions between sets.
A total function maps every element in the domain to an element in the codomain. Although not every element in the codomain may necessarily be mapped too. So, in this way functions between sets are not necessarily symmetrical.
From this mathematical structure is genererated.
Bijective functions are invertible. See: |
 |
 |
Surjective functions are not invertible in that we can't reverse the function and get back to where we started, for instance if we have a surjective mapping from set to set we can't get back to the same set, however we can go back to a 'set of sets'. This gives rise to interesting structure, see: |
 |
 |
Injective functions gives a subobject structure. If we have an injective mapping from set to set we can't get back to the same set, however we can have a mapping from set to Bool which tells us which element are in the subset, this is known as a characteristic function in sets or 'subobject classifier' more generally in category theory. This subobject structure is interesting see:
|
 |
 |
This page explains bijection, injection and surjection.
Further Topics
We can now go on and look at specific structures in more detail:
