On there pages we are looking at mathemaical structures that, often, consist of a set with aditional structure.
On this page we look a ordering. this 'ordering' is not necessarily 'numerical', for example, we can look ar the structure of subsets if set 'A' is a subset of set B we would usually denote this by A![]() B but we could denote this by A≤B or A->B to represent it as an ordered set.
B but we could denote this by A≤B or A->B to represent it as an ordered set.
Examples of the structures we will look at are:
- finite preorder.
- partially ordered sets (posets).
- chain.
- directed set (directed preorder)
- directed complete partial orders (dcpo or dcpos)
- w-continuous poset (wcpos)
- lattices
- join-semilattice
- meet-semilattice
- totally ordered set
Hasse Diagrams
We can represent set as points on a plane and the '≤' relationship as an arrow. In a Hasse diagram we don't usually show the arrow heads on the lines, instead we put the higher value closer to the top of the diagram. However, here we show the arrow heads for extra emphisis.
| For example a total order such as a set of numbers fro 0 to 5 could be shown like this: | |
| Subsets of a set have an order like this: |  |
| A more general preoder might be shown like this. | 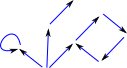 |
Properties of Order Relationships
The following properties may, or may not, apply to order relationships:
reflexive |
a≤a If a relationship is reflexive then there is always an arrow from an element of a set to itself. Although when drawing the Hasse diagram we may not draw it to avoid clutter. |
transitive |
if a≤b and b≤c then a≤c This is like composing functions. That is: if the is an arrow from 'a' to 'b' and an arrow from 'b' to 'c', then we can attach the tip of the first arrow to the second arrow to get an arrow from 'a' to 'c'. |
symmetric |
if a≤b then b≤a If a relationship is symmetric then the relationships are two-directional so its not really an order relationship. Equivalences are symmetric,more information on page here. Example: This applies to '=' but not '≤'. That is: if a=b then b=a but not necessarily: if a≤b then b≤a. |
antisymmetric |
if a≤b and b≤a then a=b |
Program issues
Do we think of sets in terms of the elements being the main focus with the set being a collection of them? Or do we think of the set being the main focus and the elements being part of it?
For instance we need to be able to define operations on the set:
a:% <= b:%
In this case '\%' is an element of the set.
We also need to define operation on the whole set, like:
subset:% := clasifier(x,set:%)
In this case '\%' is the whole set.
Some classes of ordered sets
Below we define the ordered sets.
Preorder
A (finite in this case) set equiped with a binary relation '<=' which is
- reflexive: a<=a
- transitive: if a<=b and b<=c then a<=c
In category theory a preorder only has, at most, one arrow between any two objects. (see page here).
Poset
A (finite in this case) set equiped with a binary relations '=' and '<=' which obey the following axioms:
- reflexive: a<=a
- transitive: if a<=b and b<=c then a<=c
- antisymmetric: if a<=b and b<=a then a=b
That is, it is a preorder which is antisymmetric. So it has an equals '=' relation which is defined by the '<=' relation.
Some definitions for posets which involve subsets:
If 'A' is a subset of 'X' then:
- upperBound - This is an element 'x' where for every element 'a' then a<=x.
- lowerBound - This is an element 'x' where for every element 'a' then x<=a.
- greatestElement - This is an element 'x' where it is an upperBound and it is a member of A
- leastElement - This is an element 'x' where it is an lowerBound and it is a member of A
- maximal - an element 'a' if for every element 'b' of A then if b<=a implies b=a
- minimal - an element 'a' if for every element 'b' of A then if a<=b implies b=a
- meet - a meet of two, or more, elements (in the general case the subset A) if it exists is the greatest lowerBound or infirmum.
- join - of A , if it exists, is the least element in the set of upperBounds for A.
The existance of meets and joins for subsets of preordered sets is known as:
- if meet exists - called completeness.
- if join exists - called cocompleteness.
Theorem
A poset contains no cycles.
Chain
A chain is a preorder if for every x and y we have either x<=y or y<=x.
Lattice
A lattice is a preorder which has finite meets and joins.
More about Lattice on page here.
Join-semilattice
A join-semilattice is a preorder which has finite joins.
Meet-semilattice
A meet-semilattice is a preorder which has finite meets.
Boolean lattice
A boolean lattice is a distributive lattice which also has compliments of
all elements.
Heyting lattice
A Heyting lattice is a lattice for which each pair of elements: y,z there is an element y=>z such that:
x <=y => z iff x /\ y <= z.
Every boolean lattice is a Heyting lattice.
directed set (directed preorder)
A subset 'A' of a preorder 'X' is 'directed' if it is non empty and each pair of elements in 'A' has an upperBound in 'A'.
A subset 'A' of a preorder 'X' is 'ideal' if it is non empty and each pair of elements in 'A' has an lowerBound in 'A'.
directed complete partial orders (dcpo or dcpos)
A partially ordered set is a directed-complete partial order (dcpo) if
each of its directed subsets has a supremum.
Every finite poset is a dcpo
w-continuous poset (wcpos)
w-continuous poset (wcpos) is a poset in which every w-chain
(x1<=x2<=x3<=x4<=...) has a supremum.
Every dcpo is an wcpos, since every w-chain is a directed set.
Implementation Issues
Before attemping this code I looked at the existing codebase in case I was duplicating anything that I could use. I found the following:
In catdef.spad.pamphlet I found:
\begin{itemize}
\item category PORDER PartialOrder
\item category ORDSET OrderedSet
\end{itemize}
PORDER is transitive and reflexive but no mention of antisymmetric, should
it really be preorder?
These categories do not allow an arbitary finite set to be defined so I
don't think that I can use them?
In setorder.spad.pamphlet:
\begin{itemize}
\item package UDPO UserDefinedPartialOrdering
\item package UDVO UserDefinedVariableOrdering
\end{itemize}
These packages have the usual minimal level of documentation so I don't
really know how they are intended to be used. They are packages rather than
domains so I don't really think I can use them?
In set.spad.pamphlet:
The domain SET Set has complete sets as its representations so, although
it can contain OrderedSet, I don't see how to use it here?
I think we need the representations here to be elements of the
set so that we can have operations like '<=' and '<'.
Here we implement all these finite order relations as finite graphs with
various constrains added. It would have been good to build the domains
constructivly but I can only think of a way to do it by starting with the
very general case of a graph and subtracting capability (adding constraints)
to build the more specific structures.
We map the '<=' relation to the edges in the directed graph as follows:
a b (a<=b)=false (b<=a)=false
a--->b (a<=b)=false (b<=a)=true
a<---b (a<=b)=true (b<=a)=false
a<-->b (a<=b)=true (b<=a)=true
I would have liked to use '<=' for 'less than or equal' and '<' for 'less than' and so on, but we need to specify the set that it is applied to and these are binary operations, so that won't work.
My next thought was to define it like this:
\begin{verbatim}
"<=": (n:S,%, %) -> Boolean
\end{verbatim}
but that fails with the following (unhelpful) error message:
\begin{verbatim}
>> Apparent user error:
bad == form
\end{verbatim}
So I had to use the following notation:
\begin{itemize}
\item 'lt(n,x,y)' means 'x < y' in set 'n'
\item 'gt(n,x,y)' means 'x > y' in set 'n'
\item 'ge(n,x,y)' means 'x >= y' in set 'n'
\item 'le(n,x,y)' means 'x <= y' in set 'n'
\end{itemize}
Which is horrible notation but it is the best that I can do with the
current version of FriCAS
\section{FPORDER FinitePreOrder}
<<category FPORDER FinitePreOrder>>=
)abbrev category FPREORD FinitePreOrder
++ Author: Martin Baker
++ Description:
++ based on PORDER in catdef.spad.pamphlet which is a
++ class of partially ordered sets, that is sets equipped with
++ transitive and reflexive relation \spad{<=}.
FinitePreOrder(S) : Category == Definition where
S : SetCategory
Definition ==> Join(CoercibleTo(OutputForm), SetCategory) with
lt: (n:S,%,%) -> Boolean
++ x < y is a less than test.
gt: (n:S,%, %) -> Boolean
++ x > y is a greater than test.
ge: (n:S,%, %) -> Boolean
++ x >= y is a greater than or equal test.
le: (n:S,%, %) -> Boolean
++ x <= y is a less than or equal test.
add
ge(n:S,x:%,y:%) == le(n,y,x)
-- impliments x >= y == y <= x
gt(n:S,x:%,y:%) == lt(n,y,x)
-- impliments x > y == y < x
lt(n:S,x:%,y:%) == le(n,x,y) and not(le(n,y,x))
-- impliments x < y == x <= y and not(y <= x)
@
\section{FPORDER FinitePartialOrder}
<<category FPORDER FinitePartialOrder>>=
)abbrev category FPORDER FinitePartialOrder
++ Author: Martin Baker
++ Description:
++ based on PORDER in catdef.spad.pamphlet which is a
++ class of partially ordered sets, that is sets equipped with
++ transitive, reflexive and antisymmetric relation \spad{<=}.
PartialOrder(S) : Category == Definition where
S : SetCategory
Definition ==> FinitePreOrder(S) with
eq: (n:S,%,%) -> Boolean
++ antisymmetric: if x<=y and y<=x then x=y
add
eq(n:S,x:%,y:%) == le(n,x,y) and le(n,y,x)
-- x = y == x <= y and y <= x
-- antisymmetric: if x<=y and y<=x then x=y
@
\section{domain FPO FinPreOrd}
<<domain FPO FinPreOrd>>=
)abbrev domain FPO FinPreOrd
++ Author: Martin Baker
++ Date Created: November 2013
++ Date Last Updated: November 2013
++ Basic Operations:
++ Related Constructors:
++ Keywords: finite pre order poset
++ Description:
++ finite partial order
++
++ References:
++ http: //www.euclideanspace.com/maths/standards/program/mycode/discrete/graph/
FinPreOrd(S) : Exports == Implementation where
S : SetCategory
--Exports ==> Join(DirectedGraph(S),FinitePreOrder(S))
Exports ==> FinitePreOrder(S)
Implementation ==> DirectedGraph(S) add
--le(n:S,x:%,y:%) == routeNodes(s, x, y) ~= []
--le(n:S,x:%,y:%) == routeNodeRecursive(s, x, y, []) ~= []
le(n:S,x:%,y:%) == true()
@

