Type Theory and Set Theory
Type theory and set theory have some similarities as they can be thought of as some sort of container containing a collection of elements but they have important differences:
Set Theory
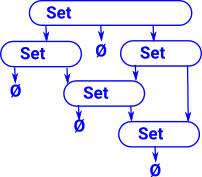
There are various formulations of set theory. In, say the ZF formulation, everything is a set. The elements of a set are themselves sets and their elements are sets. Its sets all the way down until we get to an empty set.
Also an element cannot occur more than once in a set so a given set can't contain more than one empty set.
An element can occur in more than one set but loops would allow paradoxes.
In order to prove things about sets we need a logic layer underpinning it. |
 |
Type Theory
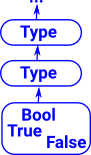
Elements of a type (terms) are unique to that type, they can't appear outside it. So, for example, the same element can't be a element of two different types.
Elements of a type can optionally be types themselves but, as with sets, a type must not contain itself. That is, it must be a strict hierarchy (no loops). See type universes. Every element has one type, types also have a type, its types all the way up. Again we can't have loops so the types must be in a hierarchy to avoid a paradox like a type of all types.
Proofs can be done within type theory using Curry-Howard correspondence. See pages about equalities. This means we don't need a separate logic to underpin type theory. |
 |
ref nlab
We can look at types from a mathematical or a computing point of view:
Types in Computing
In computing we think of type as representing some type of data structure, this determines:
- How the memory is allocated to store the type.
- Type Safety - Allows checks to be made on what operations can be done on the data to provide some level of program validation.
| See these pages for types as related to programming: |
|
With the simpler type theories: types are usually checked at compile time and elements are calculated at runtime. However when we move on to more complicated type theories such as dependent type theory (DTT) this separation get a bit blurred as explained later.
When used in a certain way, types have the same structure as mathematical proofs (see Curry-Howard correspondence). This means that, when coding these structures, in computers, we can use the same machinery to compile the algebra and the proofs. Unlike in set theory which is built over logic.
- Propositions can be represented by types which can only be constructed if they are true. That is an inhabited type can represent a true proposition, an uninhabited type is unproven.
- Proofs can be represented by functions between these types. These functions are not intended to be run (evaluated), the compiler can ensure that it is only possible to compile such a proof if it produces an inhabited type. This gives a proof system that is available at compile-time rather than run-time.
Types in Mathematics
| Types were originally added to set theory to try to resolve some paradoxes that arose. |
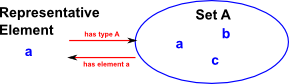 |
Another way to look at it:
A type is the range of significance of a variable, that is, the concept of a variable is tied up with the concept of a type.
Type Theories
Here are some atomic mathematical types with some examples of terms that may inhabit those types:
| Type |
Term |
|
| Boolean |
True
False |
|
| Natural Numbers |
0,1,2... |
|
| Real Numbers |
0.582 |
|
| Set |
a |
|
Type is a collection of terms having some common property.
Terms are values (or variables, or functions like the sum of other terms).
We can think of types as classifying values. If we know the type of something we have less information than knowing its value (and also its type). If we know a value without knowing its type, for example 0 (zero) we don't know if it is a natural number, or an integer, or a real number. Hence we don't know what operations might be valid to apply to it.
Types and terms are a similar (but different) concept to sets and elements. In both cases we think about it as a container relationship.
The ':' colon symbol is used to declare the type of a given term:
| Type |
Term |
|
| M |
x:M |
typing declaration |
If the type is not declared, it can be inferred in some circumstances.
We can have a multiple level hierarchy of types. For instance, the type 'M' in the above table may itself have a type of 'Type' ( M:Type ). However giving all higher order types the type of 'Type' could theoretically lead to circular references and hence paradoxes. Some theories allow these 'Type's to be numbered to enforce a hierarchy of universes and prevent any circular references. (see kinds)
Martin-Löf Type Theories
There are a number of type theories developed by Church, Martin-Löf, etc. Such as:
- STT - Simple Type Theory.
- PTT - Polymorphic Type Theory.
- DTT - Dependent Type Theory.
When working with mathematical types, especially when we are using static typing, we need dependent types. For example vectors and groups can be represented by types that depend on a value. Also fibre bundles are an important concept in mathematics that correspond to dependent types.
So here we will concentrate on dependent type theories and specifically the Martin-Löf and homotopy type theories shown below. These 3 flavours of type theory have different uses, depending on the way properties are preserved under different definitions of equalities.
| |
ETT
Extensional Type Theory |
ITT
Intentional Type Theory |
HoTT
Homotopy Type Theory |
| Equality Used |
Exact equality (after normalisation) |
Leibniz equality |
Equivalence |
| |
see page here |
see page here |
see page here |
In M-L extensional type theory two types are the same only if they are defined in exactly the same way. This becomes very important for dependent types, for example, vectors can only be added if they have the same length, however (Vect n) and (Vect (n+0)) would be treated as different types in extensional type theory. This means that extensional type theory limits the calculations and checks that can be done.
In M-L intentional type theory two types are the same if they are defined in the same way or if there is a proof that they are equal. However, in intentional type theory, proofs are not canonical for instance to construct a proof we may have to make expressions more complicated before we can simplify them. So there is not a general algorithm for constructing proofs and each proof required may have to be supplied by a human coder.
In homotopy type theory proofs are canonical (canonicity) and therefore automatic but to get this benefit other things get more complicated (conservation of complexity?). In homotopy type theory structures are built constructively rather than having constraints in the form of equations instead we have rules. The intuition for this type theory comes from homotopy.
W-Types
For more about W-types see page here.
These types can be defined by the type signatures of constructors only, this allows types to be constructed and proofs to be checked by computers at compile time rather than runtime.
So this is a 'free' construction.
Not all types can be defined in this way but where they are they are initial.
Examples of W-types are Nat, List, Tree.
For example Nat is defined like this:
That is a list of constructors defined recursively. |
data Nat : Type where
Z : Nat
S : Nat -> Nat |
Category Theory and Type Theory
We can relate type theory to category theory by linking:
- types to objects
- terms to arrows
| So if a category has various objects each of these could be related to a type. |
 |
More about linking category theory and type theory on this page.
Constructors and Eliminators
The constructors and eliminators of a type, along with the other constructs here, uniquely specify the type.
For a fuller discussion of Constructors and Deconstructors (Introduction and elimination rules) see the page here.
| There may be many ways that a given type might be constructed: |
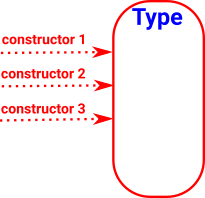 |
| The constructor or constructors for a given type should be the minimum constructor(s) that allows any other possible constructor to be channeled through it. |
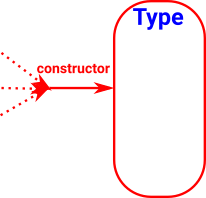 |
| The same principles apply to eliminators with the arrows reversed. |
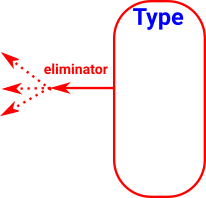 |
Constructors and eliminators can also used to prove things about the type. To do this for free objects we require:
- Local soundness of a logical connective - ("Not too strong"/"No junk"). We should not be able to prove more than our basic premises using the introduction and elimination rules of a connective (Logical connectives. The main ones are “and”, “or”, “not” and “implies”).
- Local completeness - ("Not too weak"/"No noise"). We should be able to recover the original premises through the elimination rules of the connective after using the introduction rules.
Another way to look at this, in category theory terms
Local soundness and local completeness are the triangle identities of the adjunctions that define logical connectives .
No junk and no noise are also represented by the triangle identities of the free-forgetful adjunction.
Examples
| Type |
Adjunction |
0 (empty)
A set with zero elements. |
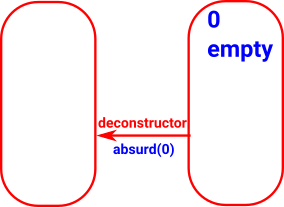 |
1 (unit)
A set with one elements. |
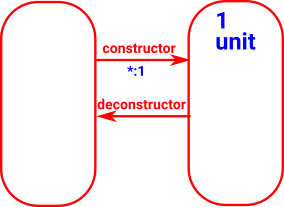 |
2 (bool)
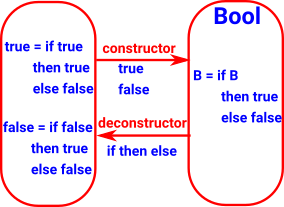
A set with two elements. This is the data type of Boolean algebra). It is like sum (either) where the terms are not necessarily types.
Like sum (either) the deconstructor requires a type 'C' and map a map from each of the elements to C. In practice we can implement this as a case-statement or even an if-then-else. |
 |
| Nat |
 |
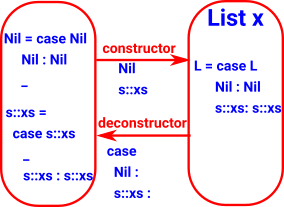
List
(free monoid) |
 |
| Sum + |
 |
| Product × |
 |
Function
Constructor (β-conversion) is lambda function, destructor (η-conversion) is function application (substitution).
Related to building and evaluating an expression, lambda calculus adds the concept of binding a variable. |
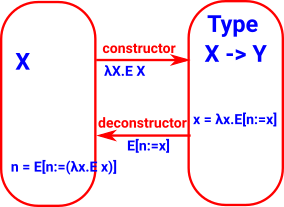
where:
- E x is an expression in x
- E[n:=x] is substitute n for x in E
|
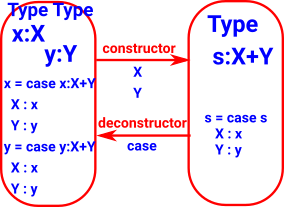
| Dependent Sum Σ |
 |
| Dependent Product Π |
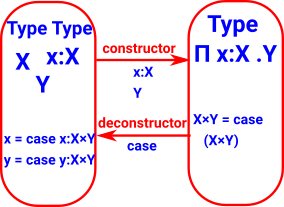 |
For every pair of terms there is an identity type. If these two terms are equal the type can be constructed by Rafl
Equality |
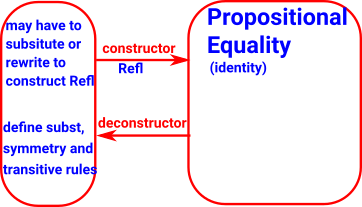 |
| |
|
| |
|
| |
|
| |
|
| Type Name |
Type Constructor |
Constructor |
Eliminator |
|
for more details click on link below |
formation |
constructors |
deconstructors |
notes |
| 0 |
|
|
|
empty
cannot be constructed
initial object |
| 1 |
|
|
|
unit
terminal object |
| Bool |
|
True
False |
conditional expression
if then else |
|
| inductive datatypes |
|
|
induction principle |
|
| Nat |
|
Z
S n |
elim_Nat: (P : Nat -> Set) -> P Z ->
((k : Nat) -> P k -> P (S k)) ->
(n : Nat) -> P n
where:
- P n = property of number n
- Z = zero
- S n = successor to n
elim_Nat P pz ps Z = pz
elim_Nat P pz ps (S k) = ps k (elim_Nat P pz ps k) |
|
| List |
|
cons |
car
cdr |
|
| Pair |
Pair |
(a,b) |
fst
snd |
|
| Function |
|
λ |
function application |
|
| Expression |
Atom |
|
|
|
| Equality |
(≡) : t->t->Type |
refl
:
{
A
:
Typei } ->
(
x
:
A
)
->
x
≡
x |
J : { A :Typei } ->
(P: (x y :A) -> x ≡ y -> Typej ) ->
( x
. P x x ( refl x )) -> x
. P x x ( refl x )) ->
 { x y } . ( eq : x ≡ y ) ->P x y eq { x y } . ( eq : x ≡ y ) ->P x y eq |
|
| + |
|
|
|
sum |
| Record |
|
tuple |
projection |
|
| × |
|
|
|
product - special case
of dependant product |
| Π |
|
|
|
dependant product
space of sections |
| Σ |
|
|
|
dependant sum |
| |
|
|
|
|
For eliminator, for inductive types we can use a recursor.
Syntax
History: start with type theories with special types for natural numbers and truth values.
(see Lambek&Scott p129)
If A and B are valid types then we can define:
where:
- φ(a) is a term of type Ω (proof of type A ??, extension of power set ??)
Product and Sum Types
Product and sum types construct a type from 2 (or more) types (A and B).
Product Type
Has one constructor (formation) and multiple ways of deconstructing (elimination) (projections).
|
 |
Sum Type
Has multiple constructors but only one way to use it. |
 |
In type theory types are defined in terms of:
- Type formation
- Term introduction
- Term Elimination
This picture shows how programming language constructs (In this case: Idris) relate to this theory: |
 |
Sum, Product and Exponent
A type theory with Sum, Product and Exponent type is related to a Cartesian Closed Category (CCC).
A term may be represented by some variable such as x,y... or a compound term using the following:
If 'M' and 'N' are valid terms, then the following are also valid terms:
| |
Type |
Term |
|
| |
|
M[x] |
We will use this notation to denote a term 'M' with multiple values depending on the value 'x'. |
| Sum |
A \/ B |
<M,N> |
This is a union of the two types. An instance will contain an instance of only one of the types.
|
| Product |
A /\ B |
(M N) |
This contains both of the types (like tuples) . An instance will contain an instance of all of the types.
We can recover the contained types as follows:
|
| Exponent |
A->B |
λ x:M.N |
This is a function from M to N.
where x is an instance of 'M' and the function returns an instance of 'N'
See lambda calculus. |
Where:
- M,N are terms, that is a base type or a compound type made up as some combination of the above. That is, they are inductively defined.
- x is an instance of 'M'
Here are some more atomic types, this time denoted in a more category theory way:
| Type |
Term |
|
| 0 |
⊥ |
empty type (initial) |
| 1 |
⊤ |
unit type (terminal) |
| 2 |
True
False |
boolean |
Semantics
To put this in a slightly more formal setting see semantics page.
Dependent Types
see this page
Recursive and Co-recursive Types
see this page
Type Theory and Logic
There are various approaches to this:
- Curry-Howard correspondence.
- A logic is a logic over a type theory.
Curry-Howard
There is a relationship between computer programs and mathematical proofs, this is known as the Curry-Howard correspondence.
A type in λ-calculus has the same mathematical structure as a proposition in intuitionistic logic.
A constructor for that type corresponds to a proof of the proposition. The following table has some specific types with their corresponding propositions:
| Proposition |
Type |
| true formula |
unit type |
| false formula |
empty type |
| implication |
function type |
| conjunction |
product type |
| disjunction |
sum type |
| universal quantification |
generalised product type (Π type) |
| existential quantification |
generalised sum type (Σ type) |
Logic over a Type Theory
We treat logic as a meta-mathematics, that is a layer above the mathematics that allows us to apply axioms and rules to prove things about the mathematics.
Type Theory and Information
Informally we sometimes think about 'information' when discussing types. for instance, does some particular operation loose or gain information. The concept of information was precisely defined by Claude Shannon in 1948. It is linked to the concept of 'entropy' which quantifies the amount of uncertainty involved. However something involving probabilities doesn't seem to be what's required here.
| So if we are trying to get an intuitive understanding of why the types/sets on the right are not isomorphic we need to see that the function shown can't be reversed. Intuitively we can see that this function 'looses information'. How can we make this more precise? |
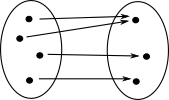 |
More specifically, in type theory we have the 'computation rule' (beta reduction rule) and the 'Local completeness rule' (eta reduction rule) - see page here. We say that the 'beta reduction rule' ensures that information is not gained and the 'eta reduction rule' ensures that information is not lost.
One way to think about this is as a constructor as a producer of information (particle of information) and as an evaluator as a consumer (anti-information) which collide and annihilate in computation and local completeness rules.
Comprehension
Any collection of elements of the same type may form an object of the next higher type.
 z'
z' x[x
x[x z <-> Φ(x)]
z <-> Φ(x)]
Concepts related to Type
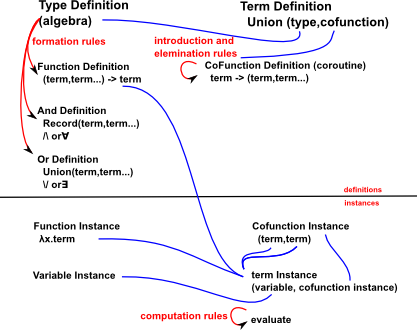
β Reduction
In type theory, β-reduction is a process of 'computation', which generally replaces more complicated terms with simpler ones.
Example of Cut elimination / substitution
In its most general form, β-reduction consists of rules which specify, for any given type T, if we apply an “eliminator” for T to the result of a “constructor” for T, how to “evaluate” the result. (n-Lab)
|
Function evaluation is called β-reduction. This is done by substitution. |
Frank Pfenning - Proof Theory Foundations, Lecture 2
| Here we show deconstruct followed by construct for Product, Sum and Exponent types: |
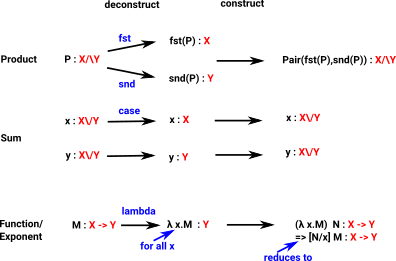 |
η Reduction
In type theory, η-conversion is a process of 'computation' which is 'dual' to β-conversion.
Whereas β-reduction tells us how to simplify a term that involves an eliminator applied to a constructor, η-reduction tells us how to simplify a term that involves a constructor applied to an eliminator.
In contrast to β-reduction, whose “directionality” is universally agreed upon, the directionality of η-conversion is not always the same. Sometimes one may talk about η-reduction, which (usually) simplifies a constructor–eliminator pair by removing it, but we may also talk about η-expansion, which (usually) makes a term more complicated by introducing a constructor–eliminator pair.
η-reduction is ill-defined for the unit type (n-Lab) .
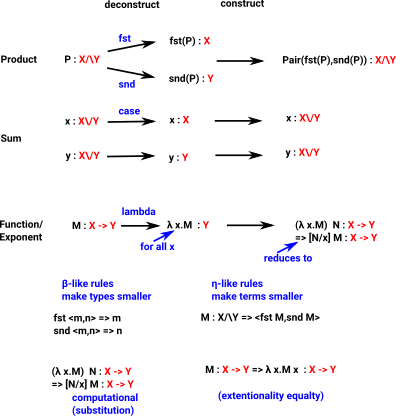
Examples from Idris
More examples on this page
Product Type
| Here we start with a product type 'M'. We can deconstruct it by using 'fst' and 'snd' then construct it to get back to 'M' |
Idris> :let M = MkPair 2 "2"
Idris> MkPair (fst M) (snd M)
(2, "2") : (Integer, String)
|
| Here we start with two terms 'x' and 'y' if we first construct using MkPair then deconstruct we get back to 'x' and 'y'. |
Idris> :let x = 3
Idris> :let y = "3"
Idris> fst (MkPair x y)
3 : Integer
Idris> snd (MkPair x y)
"3" : String |
Sum Type
| We can't constuct terms as easily because its more difficult to infer the type. |
Idris> :let M = Either Integer String
Idris> M
Either Integer String : Type
Idris> the M (Left 4)
Left 4 : Either Integer String
Idris> :let m = the M (Left 4)
Idris> m
Left 4 : Either Integer String
|
| 'case' as deconstructor |
lookup_default : Nat -> List a -> a -> a
lookup_default i xs def = case list_lookup i xs of
Nothing => def
Just x => x |
Exponent Type
| An element of A->B can be represented as λ a.Φ |
λ a.Φ : A->B |
β-reduction
The second form allows us to change the name of the variable by substitution.
Replaces a bound variable in a function body with a function argument - inlining. |
(λ a.Φ) a = Φ
(λ a.Φ) x = [a/x]Φ |
| η-reduction |
f = (λ x . f(x)) |
We cam implement in Idris like this:
We create anominous lambda like this and apply it like this.
|
Idris> \x => prim__toStrInt x
\x => prim__toStrInt x : Int -> String
Idris> (\x => prim__toStrInt x) 3
"3" : String |
Computations in Idris
A function tends to deconstruct types, rearange and do computations on the terms and then construct the output types.
| The deconstruction tends to be done by a 'case' construct in the form of pattern matching on the left hand side. |
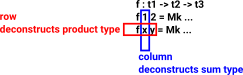 |

























