This is a branch of mathematics called group theory. A group is any set of objects with an associated operation that combines pairs of objects in the set. In other words a group is defined as a set G together with a binary operation. We will use * (or sometimes 'o') to denote the operation although this does not imply that groups only apply to multiplication. An example of a group might be the set of all integers with the operation of addition.
Groups provide a level of abstraction apart from mathematical notations. For example, rotations might be modeled by matrices or by quaternions or by multivectors or by some other notation, however we may wish to study the properties of rotations without getting involved with the mechanics of matrices etc. Groups alone wont allow us to do the calculations but they do allow us to categorize the properties of rotations in this example.
There are many types of groups:
- Groups with a finite number of objects such as MOD(N).
- Groups with an infinite number of objects such as R(2)
- Groups that are continuous (Lie groups)
We might think of groups as a set (finite or infinite) plus extra structure which is an operation that takes two elements of the set to give another element of the set. This 'composition law' turns a set into a group.
Symmetry
It is often possible to understand mathematical and physics structures by understanding their symmetries.
These symmetries are groups or, to put it the other way round, groups represent symmetries. This allows us to formalise symmetry see this page.
| Group Family | Type of Symmetry | Example | ||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cyclic | 'n' way rotation in finite steps in a plane. | Square can be rotated to four positions | ||||||||||||||||||||||||||||||
| Alternating | finite step rotational symmetry of the n-simplex in 'n' dimensions. | Tetrahedron in 3 dimensions | ||||||||||||||||||||||||||||||
| Lie | continuous symmetry
|
Properties of physics are the same regardless of the orientation in 3D space of the coordinate system. | ||||||||||||||||||||||||||||||
| Sporadic | ? | ? |
Axioms of a group
In order to be a group, a set of objects plus an operation, must obey the following axioms:
- Closure law: The set of objects must be closed with regard to the operation, in other words, the result of an operation must always be an element of the set. If c = a * b then c must be an element of the set.
- Associatively: If we are combining 3 objects we can combine the first two first and then combine the result with the third or we can combine the second two and then combine the result with the first. (But we cant necessarily reverse them, see Abelian groups below). In other words; (a * b) * c = a * (b * c)
- Identity element: There is always an operation which does nothing, in other words, there is an element e in G such that e * a = a = a * e
- Inverse element: There is always a unique inverse operation, in other words, there is only one element a-1 for each a such that a * a-1 = e. There is an element b in G such that a * b = e = b * a
Note: that there is no requirement for commutivity, that is a*b need not in general be equal to b*a.
Classification of Finite Simple Groups
We will see (on these pages) that there is a sort of meta-algebra of groups, what I mean by that is that is that we can 'multiply' or 'divide' whole groups (rather than just elements of those groups) to form other whole groups. This analogy is not exact in that the rules for this type of 'meta multiplication and division' is different from the type of operations that we are used to when applied to elements of groups and rings. However it does mean that, in the same way that we can 'factorise' integers and derive the prime numbers we can 'factorise' groups into subgroups. If we can't reduce a group into subgroups (apart from the trivial case of itself and the identity element) then it is known as a 'simple group'. In the same way that the structure of prime numbers is very complicated then the structure of simple groups is also very complicated.
A subgroup of this type is known as a quotient group or factor group (a special case is the normal subgroup)
Any simple group belongs to one of the following families of groups:
- A cyclic group with prime order.
- An alternating group of degree at least 5.
- Lie groups
- The classical Lie groups, namely the groups of projective special linear, unitary, symplectic, or orthogonal transformations over a finite field;
- The exceptional and twisted groups of Lie type.
- One of 26 sporadic simple groups.
Where:
- 'order' means the number of elements in the group.
History of Classification of Finite Simple Groups
As we have seen the structure of finite simple groups is very messy, the final sporadic group was not found until 1975. Then it was not until 1981 that the proof of the classification of finite simple groups was completed, that is the proof that the categories are complete and there are no more to be discovered. This is so complicated that even after 1981 gaps in the proof were still being found and filled in. Even now we can't be sure that there in not a hidden error.
This classification proof is perhaps the largest collaborative piece of pure mathematics ever attempted. It consists of over 10,000 pages, across about 500 journal articles, by over 100 different authors from around the world, it was without precedent.
Properties of Multiplicative Groups
If multiplication is the group operation, then applying it multiple times is represented by a superscript operator. For instance: g3 is the result of applying g in succession 3 times.
This is like the exponent for groups but there are many differences. For instance, the exponent can only be a whole integer, not a fractional value.
g0 = e = the identity element
g-1 = the inverse of g
g-n = (g-1)n
It is true that:
gm gn = gm+n
(gm)n = gmn
but in general:
(g h)n ≠ gnhn
where:
m and n are integers which may be +ve, 0 or -ve.
Abelion Groups
In general, for groups, there is no requirement for commutativity, so a * b is not necessarily equal to b * a. We can consider this as an optional property, if a group does have a commutativity property it is known as an Abelion Group. Here the group operation is usually represented as '+' .
Rotation Groups
There are 4 main Lie rotation groups (I have put the full story on this page):
- SO(n) - A group of rotations in 'n' real dimensions.
- SU(n) - A group of rotations in 'n' complex dimensions.
- SP(n) - A group of rotations in 'n' quaternion dimensions.
- G2,F4,E6,E7 and E8 - A group of rotations in 'n' octonion dimensions. (only works for 5 values of n)
How can we have rotations in 'n' complex/quaternion/octonion dimensions? I think this is shorthand for an isometry group of the projective plane over the complex/quaternions/octonions.
So, for instance, SU(2) might be thought of as a group of rotations in 2 complex dimensions. Two complex dimensions (represented by quaternions) contains 4 dimensions, but we use this to represent a double cover of rotation in 3D, so we project these 4 dimensions onto 3D space.
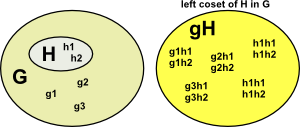
Coset and Normal Subgroup
Coset
The coset is not a group because it does not necessarily have an identity element or inverse but it is a set with an associative binary operation (this is known as a semigroup).
We create a coset from:
- A group 'G'
- A subgroup of G which we will name 'H'
- An element of G which is not an element of H which we will name 'g'
Then we can create a left coset: gH
and a right coset : Hg
gH = {gh : h an element of H} is a left coset of H in G, and
Hg = {hg : h an element of H} is a right coset of H in G.
If we were to choose the element 'g' to be an element of H then the coset would be H (since H is a group it is closed).
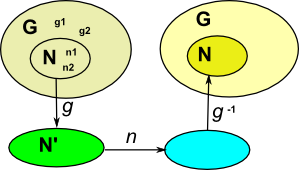
Normal Subgroup
If H is normal then:
Hg := gH.
multiplying left and right by g-1gives:
H := gHg-1
A coset is a subgroup if either:
- A subgroup where the left and right cosets are the same, or,
- A subgroup where H is preserved under conjugation.
| Coset | Normal Subgroup |
 |
 |
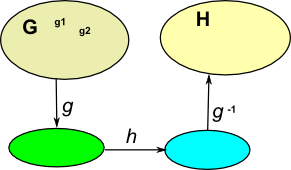
Conjugate
The conjugate is: aba-1
Not to be confused with conjugate of a complex number or quaternion.
If multiplication commutes then:
aba-1= baa-1= b
So the conjugate is a measure of how much multiplication commutes.
Notation
| notation | example | meaning |
|---|---|---|
| A | A = {a | a |
set |
| a | a |
element of A |
| {a, b, c} | set containing a, b and c | |
| a H = {ah | h |
left coset of a | |
| (a,b) | cycle notation | |
| <a,b> | all the elements of group generated by a and b | |
| <r,f | r³=1, f²=1, frf=r-1> | generators with constrains | |
| | A | | grade (size) = number of elements in A | |
| | G : H | | number of left cosets of H in G | |
| × | Direct Product | |
| Semidirect Product (left) | ||
| {n, h} |
Semidirect Product (right) | |
| Bicrossed Product also known as Knit or Zappa-Szep product |
||
a h' = h a |
Normal subgroup a H = H a for all a in G | |
| Ø | empty set | |
| ¬ | not | |
| ∧ | and ( |
|
| ∨ | or (U = union) | |
| is in (is an element of the set) | ||
| -> | if | |
| <-> | if and only if | |
| for all | ||
| there exists | ||
| is isomorphic to | ||
| orb(s) | Orbit - set of elements that can be reached | |
| stab(s) | Stabilizer - set of elements that dont move s |
More notation on this page
