On these pages we look at ways that we can construct groups from other groups. We will see that there is a sort of meta-algebra of groups, what I mean by that is that is that we can 'multiply' or 'divide' whole groups (rather than just elements of those groups) to form other whole groups. If we look at a group as a set together with a binary operation on that set, then these operations will generate both a new set and a new operation on it. The analogy with ordinary multiplication and division is not exact in that the rules for this type of 'meta multiplication and division' is different from the type of operations that we are used to when applied to elements of groups and rings.
Types of Product
On these pages we will discuss these types of 'multiplication' of groups to produce a bigger group:
Types of 'Division'
On these pages we will discuss these types of 'division' of groups to produce a smaller group:
Quotient groups and subgroups are both ways of forming a smaller group from a larger one. In category theory terms they are duals of each other.
Extension Problem
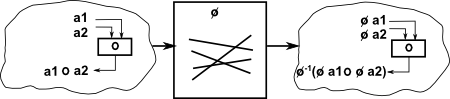
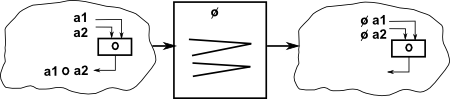
Unlike conventional multiplication and divisions, where the result of a mutiplication can be divided back to give the original operands, these group operations can not always be reversed in this way (although in many cases they can).
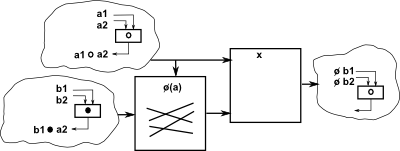
An example of where it is not possible is C4, a cyclic group of order 4, such as complex numbers which can be generated by 'i' which generates the cycle 1 -> i -> -1 -> -i. We can divide this by C2, for instance '-1' which generates the subgroup 1 -> -1 . However we cannot reverse this and generate C4 from C2
C2 and the semidirect and bicrossed products are identical to the direct product because reversing the direction of arrows in the Cayley graph does not change it.
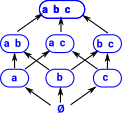
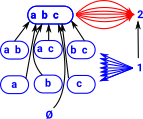
Structures
| Structure | Description |
| isomorphism |
This retains the essential structure of the group. It allows a 1:1 mapping (and its inverse) between the elements of the groups keeping the group operation the same. |
| morphism |
This is more general than an isomorphism, it allows the number of elements in the group to vary (no longer restricted to 1:1 mapping). |
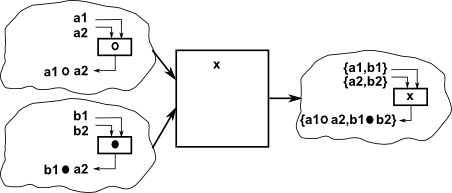
| direct product |
This combines an 'n' dimensional group with an 'm' dimensional group to give a n×m dimensional group. The group operations are applied separately. There are internal and external versions of this product. |
| permutation |
All groups can represent a permutation of a set. So it can also represent a sort of variable isomorphism, an isomorphism which is switched by another group. |
| free product | Each multiplicand is represented by a 'word' consisting of a sequence of generators. We apply the multiplication by putting the words one after the other. This is the most general type of product that contains the two multiplicands as subgroups. |
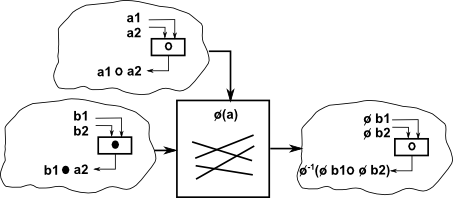
| semidirect product |
Modification of direct product using permutation. |
| bicrossed product |
 |
| division( factor group) |  |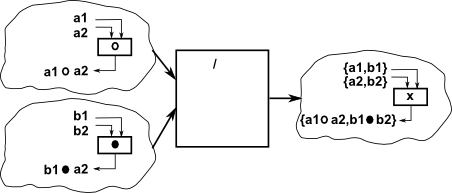
