An exact sequence consists of a sequence of algebraic structures (for instance: groups) and maps (morphisms) between these structures.
The requirement for an exact sequence is that the image of one morphism equals the kernel of the next. This has the effect that applying two consecutive maps gives the identity element.
On this page we looked at the fundamental homomorphism theorem which shows how the image of and kernel are related in a single morphism.
In a short exact sequence consisting of 5 groups the two outer groups are the trivial group consisting of the identity elements, of the remaining 3 groups the third is the second divided by the first.
Example 1
Let us take a very simple example. The first non trivial group is the cyclic group of order 2, that is C2, the next group is cartesian product of C2 and C3 which means that the last non trivial group must be C3.
![]()
We can show all the elements of these groups as follows:
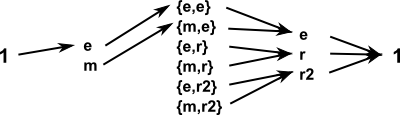
For the mapping from C2 -> C2×C3 we choose C2 ->{C2,e} and for the mapping from C2×C3 -> C3 we choose {C2,C3} -> C3.
We can see that whatever element we start with, when we apply two consecutive maps we get to the identity element.
We can also show that the image of one morphism equals the kernel of the next.
ker (1 -> C2) = e
im (1 -> C2) = e
ker (C2 -> C2×C3 ) = e
im (C2 -> C2×C3 ) = {e,m}
ker (C2×C3 -> C3) = {e,m}
im (C2×C3 -> C3) = {e,r,r2}
ker (C3 -> 1) = {e,r,r2}
im (C3 -> 1) = e
Derivation
I don't know a rigorous derivation but here is an outline:
Start by considering how we map from two groups (say C2 and C3) to their product (say C2×C3). We choose mappings between these groups such that the mappings go to the subgroup with the identity element (rather than the cosets):
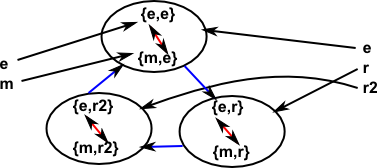
Reversing the second mapping gives:
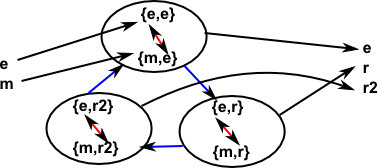
We can see that both mappings in sequence always leads to the identity element and the subgroup of the middle group is both the image of first morphism and kernel of the second.