On this page we put type theory in a slightly more formal setting, however there are many flavors of type theory and notation is not fixed so this is still general enough to allow some variants.
Judgments and Propositions
Judgment
"an object of knowledge" |
|
| proposition |
|
|
| A |
true |
|
| A |
false |
|
| t:T |
A typing declaration is something of this form
where
- t is a term.
- T is the type.
due to Curry-Howard this could be either:
- t is a proof of T
- t is a program which has type T
|
Verificationistic Meaning Theory for Intuitionistic Logic
Discusses the 'meaning' of the constructs which comes from the introduction rules.
ref
We have types and terms. A term may be either a value (a canonical term) or something that can be computed to a term.
Canonical form of function is a λ-expression. |
 |
Judgments
| a:A |
'a' is type 'A' or 'a' computes to a value of type 'A'.
'a' is a proof of 'A' |
To understand a judgment we need to know:
- when it can be correctly asserted (introduction rules)
- the consequences (elimination rules)
To understand a type we need to know:
- how it may be inhabited, what terms it has (introduction rules)
- how its terms may be used (elimination rules)
To understand a term we need to know:
- its types
- how it may be used to define other terms.
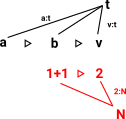
Gentzen Style Notation
ref
Assumptions
Context |
Turnstyle |
Propositions |
|
|
In a type system these are type assumptions for
the (free) term variables.
Separated by commas. All assumed to be true |
|
each one is like a parameter to a 'constructor'.
For instance 'a'
can be assigned type
A
using the type assumptions |
|
|
 |
 |
 |
|
|
| Γ,A:Type,B:Type |
 |
a:A b:B |
 |
premises |
| Γ,A/\B:Type |
 |
(a,b):A/\B |
 |
conclusion |
All premises must hold for the conclusion to be drawn.
Terms also used:
| antecedents |
A judgement on the left of the symbol. symbol. |
| succedents or consequent |
A judgement on the right of the symbol. symbol. |
| premises |
In the logic of conditionals this is called the antecedent |
| conclusion |
In the logic of conditionals this is called the consequent. |
There are variations on this notation. The diagram on the right illustrates the notation in the 'Categories for Types', Roy L. Crole book.
In this notation the syntax (function signatures) is separated from the semantics. |
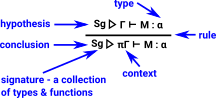 |
Here is a version from the same book for equations.
Note here equations are not shown as types in a Curry-Howard way. |
 |
Hypothetical Judgments
On the proof theory page about propositional logic (here) we have rules like the elimination rule for \/.
If A\/B then we can say that at least one of them is true. To codify this more formally we use assumptions: |
|
| The box, like this: |
[A]
...
C |
means that [A] is an assumption. |
That is, if we assume A is true then C is true. These assumptions are only temporary so we draw them in boxes to partition them off from the main sequence of logic.
So the elimination rule (\/E) says that if:
- we have a rule that proves C from A
- and we have a rule that proves C from B
- and either A, B or both are true
then C is true because we know that we can use one or both of these rules.
However, although this notation is a good way to get an intuitive understanding, the notation is a bit clumsy when part of a big proof or to use in a computer program. So in type theory, where we want to use computers, It is easier to use the concept of context.
We treat the hypotheses, or antecedents, of the judgment, J1, . . . ,Jk as temporary axioms.
Context
(ref ncatlab) A context is a list of typing declarations, in which each term is a fresh variable (i.e. one not occurring to the left of its typing declaration).
| So instead of this: |
[x:A]
...
y:B |
we can use the top judgment here: |
Γ,x:A y:B y:B |
Γ (x->y) : A->B (x->y) : A->B |
|
which is also the same as the bottom judgment. The advantage of putting the assumption x:A in the context is that it can be 'in scope' over several stages of the proof/program.
So both x y and x->y have am implication of y being derived from x.
y and x->y have am implication of y being derived from x.
Rules
Identity Rule and Cut Rule
In some way these rules give some guiding principles,
Identity Rule
we can go from assumption to conclusion. |
| |
Γa:A a:A a:A |
|
Cut Rule
This goes in the opposite direction.
This is a generalisation of 'modus ponens ' or 'implication elimination'. The cut-elimination theorem states that any judgement that possesses a proof making use of the cut rule also possesses a cut-free proof (we can inline the proof)
Sometimes the cut rule is a primitive built into the mechanism. |
|
Structural rules
Structural rules define how variables can be substituted, reordered, and ignored in appropriate ways.
| |
Rule |
Weakening Rule
Hypotheses may be extended with additional members |
Γ a:A a:A |
Γ, b:B a:A a:A |
|
Contraction Rule
Two equal (or unifiable) members on the same side of a sequent may be replaced by a single member.
Hypotheses contains two proofs of of A that is x:A y:A which we can replace with one proof z:A .
Also known as:
- factoring in automated theorem proving systems using resolution.
- 'idempotency of entailment' in classical logic.
|
Γ,x:A,y:A b:B b:B |
Γ,z:A b[z/x,z/y]:B b[z/x,z/y]:B |
|
Exchange Rule
variables in the context can be reordered. (for dependent types B cannot depend on a.) |
Γ,a:A,b:B c:C c:C |
Γ,b:B,a:A c:C c:C |
|
Substitution Rules
This rule shows how a variable can be removed using substitution.
(relationship to removing a variable by function application : lambda elimination) |
 |
| Here is the same rule for an equation. |
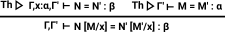 |
Rules in other Types
Information about type theories/logics which do not have some of these rules:
| |
exchange |
weakening |
contraction |
use |
| linear logic |
yes |
|
|
=1
Girard's linear logic does not allow the copying and destruction of terms so they must be used once. However they are still transferable. (transferring a resource from one owner to another can be done even when the resource cannot be copied.) |
| affine logic |
yes |
yes |
|
≤1 |
| relevent |
yes |
|
yes |
≥1 |
| ordered |
|
|
|
once in order |
λ-calculus
(see page here)
Here is a reminder of the notation:
| lambda |
variable |
dot
(separator) |
expression |
| λ |
x |
. |
2*x+1 |
Note: although I have used an arithmetic expression above, λ-terms are usually defined in a more abstract way, in the extreme case every term is a function.
T ::= V | (T T) | (λV.T)
where
- V is a variable (a symbol taken from an infinite set of symbols).
- (T T) juxtaposition is function application, different from T(T) notation.
Substitution
M[x/N]
The expression M in which every x is replaced by N
β Reduction
|
Function evaluation is called β-reduction. This is done by substitution. |
β Equality
Two terms are β-equal is one β-reduces to the other one.
M =βN
if there are terms M0 to Mn such that M0 M, Mn
M, Mn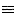 N and for all i such that 0 ≤i<n
N and for all i such that 0 ≤i<n
either: Mi =βMi+1 or Mi+1 =βMi
β-Normal Form
- M is in β-normal form if M does not contain any redux
- M is weakly normalising if there is an N in β-normal form such that M -> βN
- M is strongly normalising if there are no infinite reduction paths starting from M
Rules
In type theory there are four classes of rules:
| Rule |
Verificationist interpretation |
| formation rule |
|
| term introduction rule (constructor) |
Gives the meaning of a connective. |
| term eliminator |
How to use knowledge. |
| computation rule |
β-reduction - see below
introduction
->
elimination =
computed by
substitution
. |
| optional uniqueness principle |
η-reduction - see below |
Term introduction and eliminator rule can be chained together in two ways:
| β-reduction |
local soundness - should not gain any information |
tells us how to simplify a term that involves an eliminator applied to a constructor. |
| η-reduction |
local completeness |
tells us how to simplify a term that involves a constructor applied to an eliminator. |
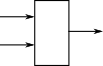
Constructor builds structure
May be multiple constructors, but only one of them is required to create a structure. |
 |
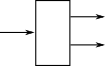
Destructor decompose structure
Often by pattern matching (case statement) |
 |
We
are choosing between A and B, if we have a constructor followed by a distructor (Beta reduction) we can either make the choice at the constructor or the distructor stage.
|
 |
 |
Recursors
Recursors can be used to make eliminators more generic, it implements pattern matching on possible values (case statement). For recursively defined types (such as natural numbers) it can be called recursively.
Recursors have the following form:
| |
|
type |
possible terms to return (may be more than one) |
value to find by matching possible terms |
| recT: |
Π |
(C |
-> T (... -> T) |
-> T) |
| C:U |
|
where
- T is the type of the recursor
- U is the universal type
|
Recursors for different types:
| type |
recursor formation and introduction |
| product |
| recA×B: |
Π |
(A -> B -> C) -> A×B ->C |
| C:U |
recA×B(C,g,(a,b)) :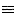 g(a)(b) g(a)(b) |
unit
(just ignore argument of unit type) |
rec1(C,c,*) :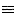 c c |
| sum |
| recA+B: |
Π |
(A -> C) -> (B -> C) -> A+B ->C |
| C:U |
recA+B(C,g0,g1,inl(a)) :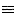 g0(a) g0(a)
recA+B(C,g0,g1,inl(a)) :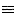 g1(a) g1(a) |
empty (bottom)
no constructor |
|
boolean |
| rec2: |
Π |
C -> C -> 2 ->C |
| C:U |
rec2(C,c0,c1,02) :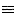 c0 c0
rec2(C,c0,c1,12) :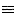 c1 c1 |
| natural numbers |
| recN: |
Π |
C -> (N -> C -> C) -> N ->C |
| C:U |
recN(C,c0,cs,0) :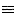 c0(a) c0(a)
recN(C,c0,cs,succ(n)) :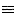 cs(n,recN(C,c0,cs,n)) cs(n,recN(C,c0,cs,n)) |
Positive and Negative types
(ref)
positive type - characterised by introduction rules (inductive type in coq).
- We construct a term using constructor.
- We use a term by saying what to do with each constructor (pattern matching).
negative type - characterised by elimination rules (example function type, dependent product).
- We use a term by applying it.
- We construct a term by saying what it does when applied.
Connectives
Conjunction and Disjunction called connectives.
Sum Type
ref
I think the + in A+B is thought of as an infix operator , we could write it as a prefix +(A,B) which makes it clearer that it is a type that depends on other types.
The usual axioms of products don't necessarily hold exactly, however they may hold upto isomorphism (or upto beta equality), that is, both sides of the equation contain the same information.
| Type |
Term |
notes |
| A+B ≠ B+A |
inl(a) =? inr(a) |
|
| (A+B)+C ≠A+(B+C) |
|
|
| A+0 ≠A |
|
0 can't be constructed so we are left with A=A |
| |
Sum Type |
formation rule |
|
| term introduction rule |
Γ a:A a:A |
|
Γ b:B b:B |
Γ inl(a): A+B inl(a): A+B |
|
Γ inr(b): A+B inr(b): A+B |
|
term eliminator rule
assume: a implies c
and b implies c |
Γ p:A+B p:A+B |
|
Γ a:A cA :C cA :C |
|
Γ b:B cB :C cB :C |
Γ match(p, a.cA b.cB):C match(p, a.cA b.cB):C |
|
computation rule
beta reduction |
match(inl(a), x.cA y.cB) =>β cA[a/x]
match(inr(b), x.cA y.cB) =>β cB[b/x] |
| Local completeness rule |
|
Implemetations of Sum
|
we could define a sum type like this:
data Or : Type -> Type -> Type where
OrIntroLeft : a -> A a b
OrIntroRight : b -> A a b
also there is a built in type 'Either': |
from : Idris-dev/libs/prelude/Prelude/Either.idr |
||| A sum type
data Either : (a, b : Type) -> Type where
||| One possibility of the sum,
||| conventionally used to represent errors
Left : (l : a) -> Either a b
||| The other possibility, conventionally
||| used to represent success
Right : (r : b) -> Either a b
-- Usage hints for erasure analysis
%used Left l
%used Right r
--------------------------------------------------------------------------------
-- Syntactic tests
--------------------------------------------------------------------------------
||| True if the argument is Left, False otherwise
isLeft : Either a b -> Bool
isLeft (Left l) = True
isLeft (Right r) = False
||| True if the argument is Right, False otherwise
isRight : Either a b -> Bool
isRight (Left l) = False
isRight (Right r) = True
--------------------------------------------------------------------------------
-- Misc.
--------------------------------------------------------------------------------
||| Simply-typed eliminator for Either
||| @ f the action to take on Left
||| @ g the action to take on Right
||| @ e the sum to analyze
either : (f : Lazy (a -> c)) ->
(g : Lazy (b -> c)) ->
(e : Either a b) -> c
either l r (Left x) = (Force l) x
either l r (Right x) = (Force r) x |
COQ
from : coq/theories/Init/Datatypes.v |
(** [sum A B], written [A + B], is
the disjoint sum of [A] and [B] *)
#[universes(template)]
Inductive sum (A B:Type) : Type :=
| inl : A -> sum A B
| inr : B -> sum A B.
Notation "x + y" := (sum x y) : type_scope.
Arguments inl {A B} _ , [A] B _.
Arguments inr {A B} _ , A [B] _. |
Product Type
ref
I think the * in A*B is thought of as an infix operator , we could write it as a prefix *(A,B) which makes it clearer that it is a type that depends on other types. These types are availible in the eliminator to be used as the types of the projections.
Terms of the product type are tuples or pairs, denoted (a,b).
The usual axioms of products don't necessarily hold exactly, however they may hold upto isomorphism (or upto beta equality), that is, both sides of the equation contain the same information.
| Type |
Term |
notes |
| A×B ≠ B×A |
(a,b) =β (b,a) |
|
| (A×B)×C ≠A×(B×C) |
((a,b),c) =β (a,(b,c)) |
|
| A×1 ≠A |
(a,()) =β (a) |
|
| |
Product Type |
formation rule
So the A×B type 'remembers' its formed from an A type and a B type? |
|
term introduction rule
(a,b) is a tuple |
Γ a:A a:A |
|
Γ b:B |
Γ (a,b) : A×B (a,b) : A×B |
|
term eliminator
Two projections fst (first) and snd (second) sometimes called p1 and p2 |
Γ t:A×B t:A×B |
|
Γ t:A×B t:A×B |
Γ fst(t): A fst(t): A |
|
Γ snd(t): B snd(t): B |
|
| computation rule, beta reduction |
fst(a,b) =>β a
snd(a,b) =>β b |
Local completeness rule
eta reduction rule
Ensures elimination rule not too weak (information not lost) |
t:A×B =>η (fst t,snd t) |
Implemetations of Product
|
We can have a type which corresponds to conjunction:
data And : Type -> Type -> Type where
AndIntro : a -> b -> A a b |
There is a built in type called 'Pair'. |
| from : Idris-dev/libs/prelude/Builtins.idr |
||| The non-dependent pair type, also known as conjunction.
||| @A the type of the left elements in the pair
||| @B the type of the right elements in the pair
data Pair : (A : Type) -> (B : Type) -> Type where
||| A pair of elements
||| @a the left element of the pair
||| @b the right element of the pair
MkPair : {A, B : Type} -> (1 a : A) -> (1 b : B) -> Pair A B |
| from : Idris-dev/libs/prelude/Prelude/Basics.idr |
||| Return the first element of a pair.
fst : (a, b) -> a
fst (x, y) = x
||| Return the second element of a pair.
snd : (a, b) -> b
snd (x, y) = y |
COQ
from : coq/theories/Init/Datatypes.v |
(** [prod A B], written [A * B], is the product of [A] and [B];
the pair [pair A B a b] of [a] and [b]
is abbreviated [(a,b)] *)
#[universes(template)]
Inductive prod (A B:Type) : Type :=
pair : A -> B -> A * B
where "x * y" := (prod x y) : type_scope.
Add Printing Let prod.
Notation "( x , y , .. , z )" :=
(pair .. (pair x y) .. z) : core_scope.
Arguments pair {A B} _ _.
Register prod as core.prod.type.
Register pair as core.prod.intro.
Register prod_rect as core.prod.rect.
Section projections.
Context {A : Type} {B : Type}.
Definition fst (p:A * B) := match p with (x, y) => x end.
Definition snd (p:A * B) := match p with (x, y) => y end.
Register fst as core.prod.proj1.
Register snd as core.prod.proj2.
End projections. |
Function Type
ref
In logic called 'implication'.
This requires the concept of substitution.
Usually defined as a 'negative type', that is we define it by how it is used (applying a function).
We can think of the type A->B as either,
- All the possible functions from type A to type B (a homset).
- Object of type B parameterised by an variable of type A.
I find it easier to understand the introduction and elimination rules in terms of the second interpretation.
| Implication is a bit like taking a whole rule, putting brackets round it and using it as a premise for another rule. |
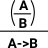 |
Notation: a function ( x |-> b(x)) can be notated using lambda symbol: λ x . b(x) using '.' to seperate input parameter from output.
| |
Function Type |
formation rule |
 A:Type A:Type |
|
 B:Type B:Type |
 A->B : Type A->B : Type |
|
term introduction rule
assume a implies b
(given a proof of A we get a proof of B) |
lambda abstraction:
Γ a:A b:B b:B |
|
Γ B:Type B:Type |
Γ λa.b : A -> B λa.b : A -> B |
|
term eliminator
Modus Ponens |
application:
Γ A->B:Type A->B:Type |
|
Γ a:A a:A |
Γ f(a) : B f(a) : B |
|
computation rule
substitution - in this case of a for x. |
( λ x . b(x)) (a) =>β b(a)
we reduce this by substitution.
b[a/x] |
Local completeness rule
eta reduction rule |
M:A->B =>η λ x. M x |
| To introduce a term of type A->B we need a free variable in A and a term of type B containing x. |
 |
Implemetations of Function Type
|
from : Idris-dev/libs/prelude/Prelude/Basics.idr |
||| Function application.
apply : (a -> b) -> a -> b
apply f a = f a
|
Other Types
Empty Type
ref
Denoted 'empty' or 0 or bottom or _|_ .
| We cannot introduce a term. If we do have a term then we can prove any other type. So we have no arrows in but we have arrows going out to every other type. |
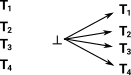 |
as a negative type:
| |
Empty Type |
formation rule
It exists |
|
term introduction rule |
There is no introduction rule |
| term eliminator |
|
| computation rule |
There is no computation rule |
Local completeness rule |
|
Implemetations of Empty
|
from : Idris-dev/libs/prelude/Builtins.idr |
||| The empty type, also known as the trivially false proposition.
|||
||| Use `void` or `absurd` to prove anything if
||| you have a variable of type `Void` in scope.
data Void : Type where
||| The eliminator for the `Void` type.
void : Void -> a
|
COQ
from : coq/theories/Init/Datatypes.v |
(** [Empty_set] is a datatype with no inhabitant *)
Inductive Empty_set : Set :=.
|
Unit Type
ref1 ref2
Denoted 'unit' or 1 or top or T .
Unit is always true, we can introduce a term without any additional information.
There is a sense that this is the inverse of the empty type:
- empty type can not be introduced
- unit type can always by introduced
|
 |
The term of the unit type is thought of as the null tuple (). This is because of the way that it works with the product type:
(x,()) =β (x)
In computing this equality does not hold exactly, however it is true upto isomorphism (or upto beta equality), that is, both sides of the equation contain the same information.
Can we use unit type to build enumeration types? Example 2=1+1. That would be more like a tuple with one element? unit(C)? which does not seem to be what we have here?
In the propositions-as-types approach the unit type corresponds to 'mere' propositions are the propositions in classical logic. This allows us to use the law of excluded middle when appropriate (for set-like structures).
The 'unit' type, in homotopy collapses to a point so, in that way, it is the most fundamental type.
| |
Unit Type |
formation rule
Unit type exists and does not depend on anything. |
| |
 unit :Type unit :Type |
|
term introduction rule
Unit is always true, we can introduce a term without any additional information. |
| |
 tt :unit tt :unit |
|
term eliminator
p:unit /\ c = c
If we know how to produce a C using all the possible inputs that can go into a unit, then we can produce a C from any unit. |
Γ ():unit ():unit |
|
Γ C:Type C:Type |
|
Γ c:C c:C |
Γ triv((),c):C triv((),c):C |
|
computation rule
When we evaluate the eliminator on a term of canonical form, we obtain the data that went into the eliminator associated with that form |
Γ C:Type C:Type |
|
Γ c:C c:C |
Γ triv((),c)->β c triv((),c)->β c |
|
Local completeness rule |
|
Implemetations of Unit
|
from : Idris-dev/libs/prelude/Builtins.idr |
||| The canonical single-element type, also known as the trivially
||| true proposition.
data Unit =
||| The trivial constructor for `()`.
MkUnit
|
COQ
from : coq/theories/Init/Datatypes.v |
(** [unit] is a singleton datatype with sole inhabitant [tt] *)
Inductive unit : Set :=
tt : unit. |
Identity Type
ref
| |
Identity Type |
formation rule
Id exists for every pair of terms in A |
 A:Type A:Type |
Γ, x:A, y:A IdA(x,y) : Type IdA(x,y) : Type |
|
term introduction rule
reflexitvity |
Γ A:Type A:Type |
Γ , a:A refl(a) : IdA(a,a) refl(a) : IdA(a,a) |
|
| term eliminator |
|
| computation rule |
|
Local completeness rule |
|
Implemetations of Identity Type
|
from : Idris-dev/libs/prelude/Prelude/Basics.idr |
||| Identity function.
id : a -> a
id x = x |
COQ
from : coq/theories/Init/Datatypes.v |
(** [identity A a] is the family of
datatypes on [A] whose sole non-empty
member is the singleton datatype [identity A a a] whose
sole inhabitant is denoted [identity_refl A a] *)
#[universes(template)]
Inductive identity (A:Type) (a:A) : A -> Type :=
identity_refl : identity a a.
Hint Resolve identity_refl: core.
Arguments identity_ind [A] a P f y i.
Arguments identity_rec [A] a P f y i.
Arguments identity_rect [A] a P f y i.
Register identity as core.identity.type.
Register identity_refl as core.identity.refl.
Register identity_ind as core.identity.ind.
(** Identity type *)
Definition ID := forall A:Type, A -> A.
Definition id : ID := fun A x => x.
Definition IDProp := forall A:Prop, A -> A.
Definition idProp : IDProp := fun A x => x. |
Boolean
We can use sum to get boolean from two units (1+1=2)
| |
Boolean Type |
formation rule
dont really need to have two copies of Unit, just making the point this is a sum. |
 Unit:Type Unit:Type |
|
 Unit:Type Unit:Type |
 Boolean : Type Boolean : Type |
|
| term introduction rule |
Γ a:Unit a:Unit |
|
Γ b:Unit b:Unit |
Γ inl(a): Boolean inl(a): Boolean |
|
Γ inr(b): Boolean inr(b): Boolean |
|
term eliminator
assume: a implies c
and b implies c |
Γ p:Boolean p:Boolean |
|
Γ a:Unit cA :C cA :C |
|
Γ b:Unit cB :C cB :C |
Γ match(p, a.cA b.cB):C match(p, a.cA b.cB):C |
|
| computation rule |
beta reduction
match(inl(a), x.cA y.cB) ->β cA[a/x]
match(inr(b), x.cA y.cB) ->β cB[b/x] |
Local completeness rule |
|
We can then add negation
Negation Rule
formation rule |
|
term introduction rule |
|
| term eliminator |
|
| computation rule |
|
Local completeness rule |
|
Bottom Rule
formation rule |
|
term introduction rule |
|
| term eliminator |
|
| computation rule |
|
Local completeness rule |
|
Enumeration Type
ref
An enumerated type is any type given by a finite disjoint sum of unit types.
Can be thought of as a sum (1+1...) or as a degenerate form of an inductive type.
Inductive Types
Natural Number Type
I have put more information about natural number types on page here.
| |
Natural Number Type |
formation rule
N exists |
| |
 N : Type N : Type |
|
term introduction rules
|
|
term eliminator
Proof by induction
To prove property P (implemented as a type) we need to proove P(0) and P(x) implies P(sx)
rec is recursor (see recursor section above) where:
rec
nat
z0 zs O
=
z0
rec nat z0 zs( S n) = zs (n ,(rec nat z0 zs, n))
where
- z0 is the value returned for zero.
- zs is the value returned for succesor.
|
x:N P(x):Type P(x):Type |
|
 p0:P(0) p0:P(0) |
|
x:N,p:P(x) ps(x,p):P(sx) ps(x,p):P(sx) |
|
 n:N n:N |
 recpn(p0.ps):P(n) recpn(p0.ps):P(n) |
|
| computation rules |
x:N P(x):Type P(x):Type |
|
 p0:P(0) p0:P(0) |
|
x:N,p:P(x) ps(x,p):P(sx) ps(x,p):P(sx) |
 recp0(p0.ps):P(0) recp0(p0.ps):P(0) |
|
x:N P(x):Type P(x):Type |
|
 p0:P(0) p0:P(0) |
|
x:N,p:P(x) ps(x,p):P(sx) ps(x,p):P(sx) |
|
 n:N n:N |
 recpsn(p0.ps):P(sn) recpsn(p0.ps):P(sn) |
|
Tree Type
Effects
(See Youtube - Oregon Programming Languages Summer School 2012, University of Oregon part 2)










