Maths - Cartesian Closed Categories

Requirements for CCC

In a category C:

• Has a terminal object.
• Any two objects X and Y of C have a product X ×Y in C.
• Any two objects Y and Z of C have an exponential Z^Y in C.

Which Concrete Categories are CCC

Cartesian closed:	Not cartesian closed:
Set	SGrp
Set × Set	VecK
Set ↓ Set	Mon
Set ↓ I, for any set I	Grp
Cat	Ab
Grph	Top

Hierarchy of Categories

These pages discuss, not just cartesian closed categories, but also a whole hierarchy of categories.

This diagram of the relationship between various categories is adapted from this John Baez paper.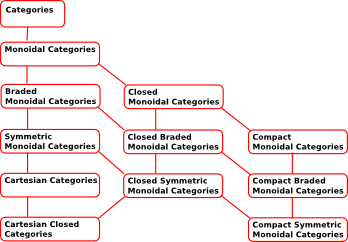

Introduction

Category diagrams can define mathematical structures, such as monoids, from the outside. Category diagrams can also define operations on those structures, such as products, which can build structures by combining existing structures. Note that the categorical product does not necessarily define the multiplication in a concrete structure like a monoid. However there is a structure, like a monoid, but whose objects are categories, this is a monoidal category.

Monoidal Category

We can catogorify the idea of a monoid by changing the equalities to isomorphisms.

Monoid	Monoidal Category
a binary operation * axioms: Associatively: (a * b) * c = a * (b * c) Identity element: e * a = a = a * e	a tensor product functor:C×C->C axioms: Associator: (ab)ca(bc) unitor: 1aaa1

Pentagon

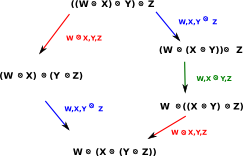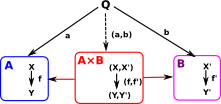
Cartesian Product

We can extend the concept of cartesian product of sets to categories as follows:

An object of A×B is a pair (X,X'). A morphism of A×B is a pair (f,f').
Composition is done componentwise: (g,g')(f,f')=(gf,gf')
Identity morphisms are defined componentwise: 1(X,X') = (1X,1X')

The arrows, between A,B,A×B and Q, on the above diagram are functors, that is, they are functions between categories that preserve some structure.

The cartesian product is not necessarily commutative or associative, although it is associative upto isomorphism.

Example - Sets {a,{b,c}} is not equal to {{a,b},c} but it is isomorphic to it.

Tensor Product

The tensor product involves the following concepts:

• Combining arrows in parallel.
• Binary functor:C×C->C.
• The most general bilinear operation.
• Carteasion product.
• Outer product.
• Co-products of frames (locales).

A tensor product (i.e. a monoidal product) is not, in general, a categorical pruduct (such as a catesian product). However, the converse is, that is a cartesian product is a monoidal product.

The tensor of A and B exists if there is an object ABC together with isomorphisms: C(AB,X)[A,C(B,X)]

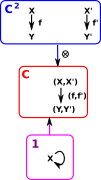Bilinear Aspect of Tensor Product

Cartesian Category

We have seen the monoidal product (tensor product) is not necessarily the same as the categorical product (carteasian product). In cases where they are the same the monoidal category is known as a cartesian category.

Examples (from this video) of cartesian categories are:

Cartesian Category	Group Object
Set	group
Top	topological group
Manifold	Lie group
Group	abelian group
Cat	crossed module

A category has finite products if it has a binary product and a terminal object.

• The binary product is the tensor product.
• The terminal object is the unit object. The unit '1' is like a product with zero parameters.

Braided Category

The string diagrams for a braided category can have a crossover.

Generalisation

Next

See page here about Cartesian Closed Category structures in graphs.

EuclideanSpace

home

Prerequisites

See this page for introduction to category theory concepts.

This page illustrates some issues from monoidal categories using graphs as an example.

There is more about graph theory on this page.

There is a program which can represent and do calculations on graph theory on this page and specifically about graph products on this page.

Categories for the Working Mathematician - This is the classic book on the subject but the pace is very quick and a wide knowledge of mathematics is required to understand the examples. Its hard going for me but then I'm not a working mathematician.

Category Theory