Maths - Equivalence

In the same way that isomorphism is like equality but weaker, equivalence tends to be like isomorphism but weaker.

However, there are many competing definitions of equivalence:

We could take two objects to be equivalent if there is an equivalence relation between them. That is, a relation that is reflexive, transitive and symmetric (see below).
In category theory (see page here) equivalence can be defined by two opposing morphisms F & G which, when composed bring objects to something isomorphic to the original.
In type theory (see page here) equivalence can be defined as a fibre into B from A which is contractible.

Equivalence Relations

The following properties apply to equivalence relations:

reflexive

a~a

If a relationship is reflexive then there is always an arrow from an element of a set to itself. Although when drawing the Hasse diagram we may not draw it to avoid clutter.

transitive

if a~b and b~c then a~c

This is like composing frunctions. That is: if the is an arrow from 'a' to 'b' and an arrow from 'b' to 'c', then we can attach the tip of the first arrow to the second arrow to get an arrow from 'a' to 'c'.

symmetric

if a~b then b~a

This applies to '=' but not '≤'. That is: if a=b then b=a but not necessarly: if a≤b then b≤a.

Instead of the symmetric property, it is possible to have an antisymmetric property:

if a≤b and b≤a then a=b

This page discusses order relationships.

Equivalence on Sets

Sets are don't have duplicate elements, so two different enlements of the same set can't be equal to each other. However we can add an equivalence relation to a set.

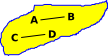	Here we have a set with 4 elements: A,B,C and D. Suppose we have the following equivalences: A~B C~D
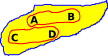	This is a bit like sets within a set, but where the outside set can 'see' the inside elements.
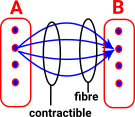
	There is also a more categorical approach to this. We could look at the external properties rather than the internal properties. We could construct a morphism to the equivalence classes.
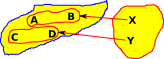	We can't construct an inverse to the above morphism (So there is not an isomorphism between these two sets). However we can map back to a set of equivalent values.

The above argument is not quite correct because an equivalence should map back to somewhere isomorphic to the starting point, not equivalent, so its not a proof of the categorical definition of equivalence.

Group Equivalences

We can use a similar argument to sets above, but this time for groups.

Left or right cosets of a subgroup partition a group. See page here.

let:

• H be a subgroup of group G.
• ~ be an equivalence relation on G
• a ~ b ↔ (ab⁻¹H).

	Group	Equivalence Relation
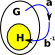		x~y
transitive	a b-1b c-1=a c -1 since b-1b=1	x~y, y~z->x~z
reflexive	if a maps to H then composing with 1 wont change that.	x~x
symmetric	The inverse of a b-1 is b a-1 If H contains a b-1 then it must contain its inverse.	x~y->y~x

 

EuclideanSpace

home

Prerequisites

This page discusses isomorphism.

Related Concepts

• This page discusses order relationships.
• Equivalence in category theory.

Equality