Maths - Oidification - Martin Baker

Oidification

Oidification allows us to start with a single object and one (or more) arrows back to itself and generalise this to multiple objects. This new structure does not need to have arrows between every pair of objects but composition always exists and every object has an identity arrow.

Here the words 'object' and 'arrow' are used in the category theory sense as described on the page here.

Here are some examples:

	Single Object	Multiple Objects
Setoid This imposes an external equivalence relation and internalises it.	The single object needs to have the reflexive relation, that is, be equal to itself. An example would be a set with a set with a fixed number of elements.	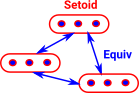Since the arrows are reflexive, symmetric and transitive this gives an equivalence relation.
Groupoid This can be thought of as a weakening of a setiod. Instead of equivalences we have isomorphisms, that is the permutations show how objects are equal in multiple ways.
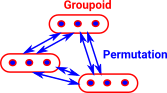Category Just to confuse things the naming conventions have changed here. Monoid has an 'oid' but this is the single object case. A Monoidoid is a category.

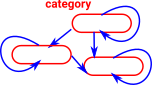Single Object

Multiple Objects

Setoid

This imposes an external equivalence relation and internalises it.

The single object needs to have the reflexive relation, that is, be equal to itself.

An example would be a set with a set with a fixed number of elements.

Since the arrows are reflexive, symmetric and transitive this gives an equivalence relation.

Groupoid

This can be thought of as a weakening of a setiod. Instead of equivalences we have isomorphisms, that is the permutations show how objects are equal in multiple ways.

metadata block

see also:	This Site Groupoid Setoid Other Sites There is an implementation of a setoid using Idris on Github.
Correspondence about this page
Book Shop - Further reading. Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.	Modern Graph Theory (Graduate Texts in Mathematics, 184)
Terminology and Notation Specific to this page here:

Maths - Oidification

Oidification

EuclideanSpace

Related Pages

This Site

Other Sites