Maths - Sub Object

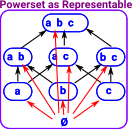
Set Since topos theory is about set-like structures lets look at set first and then generalise to other topoi. In set all the subobjects are given by the powerset.

This set of all subsets comes with some structure (poset structure), the arrows on the above diagram are inclusion maps or we can think of the arrows as meaning 'is a subset of'.

All the elements of the powerset are subsets of the set {a,b,c}. Also all the elements are supersets of the empty set ø. Therefore all the subsets are representable (in two ways), that is we can replace all the subsets with arrows.

Subobject Classifier

See .

See page here for a non-categorical approach to sub-objects.

If the arrow 'f' is monic (injective) then it maps to a subobject (subset) of 'B'. That is: there is a subobject of B that is isomorphic to A. The inclusion relation on subobjects is: reflexive transitive

In order to define the subobject we must define the monic 'upto equality' which is not in the spirit of category theory. We will go on to define a 'subobject classifier' which defines a subobject, in a much more category theoretic way, by the composition of maps (and also relates the whole subject to logic).

The classifier (characteristic function in subset case)

Subset	Classifier
ø	{0,0,0}
{a}	{1,0,0}
{b}	{0,1,0}
{c}	{0,0,1}
{a,b}	{1,1,0}
{a,c}	{1,0,1}
{b,c}	{0,1,1}
{a,b,c}	{1,1,1}

Consider the contravariant functor P : Set->Set which maps each set to its power set and each function to its inverse image map. To represent this functor we need a pair (A,u) where A is a set and u is a subset of A, i.e. an element of P(A), such that for all sets X, the hom-set Hom(X,A) is isomorphic to P(X) via Φ_X(f) = (Pf)u = f⁻¹(u). Take A = {0,1} and u = {1}. Given a subset SX the corresponding function from X to A is the characteristic function of S.

Naming Arrows

In category theory we don't usually identify elements, such as elements of a set, because we only tend to determine things 'upto isomorphism'. The objects in a category are whole 'structures', they don't represent individual elements.

However, there is the possibility to indicate elements indirectly using arrows. For instance, if we want to enter a specific element we can use:

1->A

because, in sets, 1 is the single element set so it will indicate an element uniquely.

We can also use naming arrows. An arrow:

f: A->B

Is a subset of a function spacef:{0}->B^A

fis called the 'name' of the function.

Classifier

In the opposite direction there is a correspondence between subsets of B and functions:

B->2

This is in the space 2^B which corresponds to the powerset(B), that is, all the possible subsets of B.

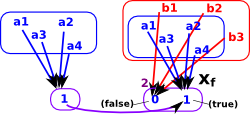
The characteristic arrow: xf classifies objects of B to determine if they are images of A. This is a pullback square. The object 2 has two values: 0 and 1. We also use the symbol Ω and call the elements 'true' and 'false'.

This means the topos theory is related to logic. (see also 'characteristic function' in number theory).

Example in Set

	Example in set
Set A (blue) is subset of B (red).
If we take the inverse of f we get the concept of a 'bundle' as discussed on this page.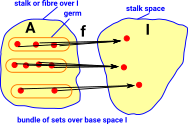
classifier for set.

Subobject and Fibre

Here we discuss combining subobject and fibre (taking part of a fibre).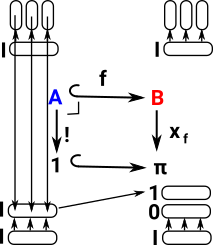
Just to explain the diagram, these two are intended tp be the same: π=(2*I,p1)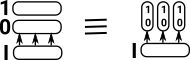

Notation

this can be donated as a pair (A,f)

I is common and does not need to be specified.

EuclideanSpace

home

Prerequisites

For non-catagorical discussion of fibre concept see the page here.

Also see: Topology and open sets.

Other Pages

Other pages on this site which discuss fibres:

• In topology terms.
• In type theory

Related Subjects

• Representables and Yoneda
• Presheaves
• Category of Presheaves
• Cubical Type Theory

Set + Structure