Language and Interpretation
The Mitchell-Bénabou language has a syntax and this can be translated into an interpretation.
The interpretation is a function. When we are dealing with logic then these are functions into the truth object Ω but they can be mixed in with other types of function.
This function into the truth object Ω is like a predicate. An example of this might be an equation like: x=3 or a predicate like even(x). These both give a value which is true or false for any given value of x. Here we are generalising from set theory/Boolean values to Topos theory/truth objects. So we have something that looks like a mapping from a set of variables to the truth object.
Mitchell-Bénabou Language
A simple form of the internal language of an elementary topos E. It makes use of the fact that in the presence of a subobject classifier Ω, there is no need to treat formulas separately from terms, since a formula or proposition can be identified with a term of type Ω.
Table
| Term | Interpretation (arrow) | |||
|---|---|---|---|---|
| T1 | Variables May be free or bound as in lambda calculus. |
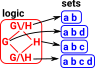
I1 | Variable xi in list For a free variable xi the interpretation is the ith projection. |
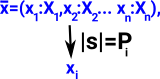 |
| T2 | Arrow f: x->y |
I2 | The interpretation of f s is f |s|. |f s| -> f |s| |
 |
| T3 | Constant c: 1->a |
I3 | The interpretation of a constant 'c' is c! | 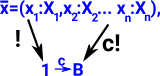 |
| T4 | Product For a term:
there is a term <s1,s2> of type A×B. |
I4 | The interpretation of a product <s1,s2> is <|s1|,|s2|> |<s1,s2>| -> <|s1|,|s2|> |
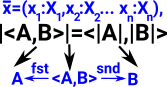 |
| T5 | Exponential For a term s of type B and a term y of type Y there is a term λ( y.Y)s of type BY. We say the variable y is bound by the lambda operator. |
I5 | |λ( y.Y)s |x,y-> <|s|x> where s is transpose of s |
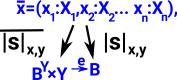 |
Transpose
The transpose above in exponential may need more explanation. See Currying.
We can replace
f(x,y) -> R
with
f(x) -> (y -> R)
which can be denoted:
f(x) -> RY
So input parameters can be removed provided the output format is changed.
Internalising Structure
In type theory an element of a type is made (instantiated) using a type constructor. Can we customise these types (build structure into the type) by having constraints in addition to the constructors?
Denoted as an extension like this:
[constructors | constraints]
An extension is the subobject classified by the map into Ω (constraints).
Similar idea to group presentation.
where each contraint is a function from the variables to the truth object (as above).
Subobject Classifier
| A subobject classifier is an arrow from 1 (terminal object) to Ω. | 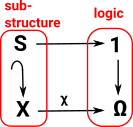 |
This is an extension. It can be thought of like a comprehension where the variables are before the '|' and the classifier (which specifies a sub-object) is after it.
| [x.X | χq(x) /\ χr(x) ] | |
| [x.X,y.Y | χq(x) /\ χr(y) ] |  |
Model Theory
All the flavours of model theory rest on one fundamental notion, and that is the notion of a formula φ being true under an interpretation I. (Wilfrid Hodges)
Theory
In model theory a 'theory' is a set of first-order sentences, for instance:
 x
x y
y z.(x+(y+z)=(x+y)+z)
z.(x+(y+z)=(x+y)+z) x.(x+0=x)
x.(x+0=x) x.(x+(−x)=0)
x.(x+(−x)=0) x
x y.(x+y=y+x)
y.(x+y=y+x)
Model of Theory
There can be multiple models of any given theory
Internal Logic
See ncatlab:
large parts of mathematics can be internalized in any category with sufficient structure
The idea is to exploit the fact that all mathematics can be written in the language of logic, and seek a way to internalize logic in a category with sufficient structure.
The basic ideas of the internal logic induced by a given category C are:
| The objects A of C are regarded as collections of things of a given type A: |  |
| The morphisms A->B of C are regarded as terms of type B containing a free variable of type A (i.e. in a context x:A) | 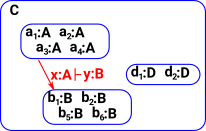 |
A subobject
|
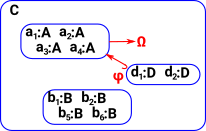 |
Logical operations are implemented by universal constructions on subobjects.
|
|
| A dependent type over an object A of C may be interpreted as a morphism B->A whose “fibers” represent the types B(x)for x:A. This morphism might be restricted to be a display map or a fibration. |
Alternative Version of Expression
variables -> truth value
x1,x2,x3...xn -> Ω
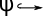 ψ
ψ