If Y and T are objects in a category then, if that category has exponential objects, then YT is also an object in the category. For example cartesian closed categories are an important class of categories that have exponential objects.
We can think of the object YT as representing all functors from T to Y:
T -> Y
Also notated Hom(T,Y) see Hom set on page here.
So exponential objects can have have properties similar to exponents in ordinary algebra.
| If we think of an exponent as 'n' copies of 'a' then this might be interpreted as a function implemented as a lookup table. | |
| an × am =an+m | If we interpret a product as a tuple and a sum as 'either' then this equality becomes: (n->a,m->a) = (either (n,m)) -> a |
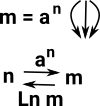 |
In ordinary number algebra the inverse of the exponential is the logarithm. There doesn't seem to be a direct equivalent of log in category theory but the representables have similar properties. |
These equalities from ordinary algebra don't always apply to exponential objects in category theory but they may apply in some reduced form, for instance:
- They may apply 'upto isomorphism'.
- They may apply in simpler categories like sets.
Example in Set
for instance in the following mapping from set to set:
 |
If we are mapping from set T to set Y and the number of elements in T is t and the number of elements in Y is y then the number of mappings from T to Y is yt. |
This also behaves like an exponent in that YA * YB = YA+B. That is, if we have 3 categories, one of which is the sum of the other 2, each has a mapping to a 4th category then these mappings will be a product. See diagram on left:
 |
 |
For a generalistion of this see Yoneda embedding.
Evaluation
In propositional logic there is a rule called 'modus ponens':
|
modus ponens |
That is: if 'B implies A' and 'B' is true then A is true.
This has a similar form to this functor:
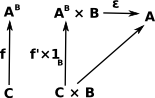
ε: AB × B -> A
In this case we will call ε 'evaluation'.
Alternativly, for any object C:
f: C × B -> A
there is a unique arrow:
f': C -> AB
The relationship between ε, f and f' is:
ε•(f' × 1B) = f
This is represented by the following diagram:
Relation to Internal Hom-set
An internal hom-set in a cartesian closed category is an exponential object.
Next Steps
- The exponent category is a Hom set which is discussed on page here.
- Hom sets are used in the page about the Yonada Lemma to relate structures at different levels of abstraction.
- The page here discuses homsets from a set theory perspective.
- Other related pages are: