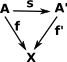
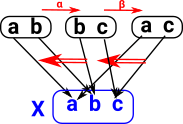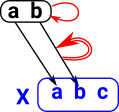Category Theory - Comma and Slice Categories

"Comma categories were introduced by Lawvere [1963] in the context of the interdefinabilty of the universal concepts of category theory. The basic idea is the elevation of arrows of one category to objects in another" - Computational Category Theory, D.E. Rydeheard R.M. Burstall.

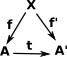
Here are some examples of comma categories. In these cases all the objects are in the same category (including the fixed object). The comma category generalises this by allowing the objects to come from other categories.

Arrow category

see page here

diagram
  • Objects f:X->I
  • Morphisms <s,t>

Examples

fibration

Slice category

see page here

 diagram
  • Objects f:X->I
  • Morphisms s
 

Co-slice category

see page here

 diagram
  • Objects f:X->I
  • Morphisms t

Examples

substitution

Slice Category

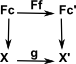
Given a category C we can 'slice' it over some object X∈C which we fix in C.

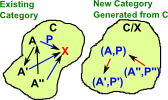
This construction allows us to start with one category 'C' and generate a different category 'C/X' by fixing a given element 'X' in C. The elements in C/X are pairs (A,P) where A∈C and P is a morphism from A to X. slice category overview

'co-slice' is the dual concept, just reverse all the arrows.

Slice Category Examples

On the page here I have put more information about these examples

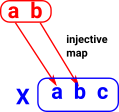
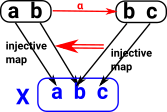
Colouring of labeled set.

Here we choose as our fixed object 'X' the 3 element set containing R, G and B (for red green and blue). Every object (in this case set) has an arrow (function) to this set so all the elements are assigned a colour.

more here

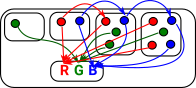 colouring example diagram

Adding a distinguished point (the origin) to Euclidean space to give a vector space.

more here

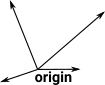Comma Category

In the slice category all the objects are in the same category (including the fixed object).

The comma category generalises this by allowing the objects to come from other categories.

comma category diagram

Special Cases of Comma Category

We have already seen the slice category, here is a fuller list of special cases and related constructs:

Slice Category

If 's' is the identity functor of C and 't' is the inclusion 1 -> C of an object c∈C, then (s/t) is the slice category C/c.

See ncatlab site.

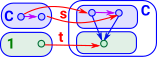 slice diagram

Co-slice Category

Likewise if 't' is the identity and 's' is the inclusion of c, then (t/s) is the coslice category c/C

See ncatlab site.

 coslice diagram

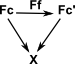
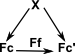
Arrow Category

This is all derived from a single category. So it is a comma category where the arrows into it are identity functions. Unlike the slice or co-slice both the source and target can be somthing other than the terminal object.

  • An object 'a' of Arr(C) is a morphism a:a0->a1 of C
  • A morphism f:a->b of Arr(C) is a square.

See page here, see also functor category page here.

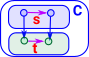 arrow category diagram

Graph Category

The category of graphs is an example of a comma category, that is, a graph is isomorphic to a comma category. Arrows of graphs are pairs of functions mapping nodes to nodes (N -> N) and edges to edges (E -> E) , an object of this category it a triple (E,f: E -> N×N,N) where f maps each edge to a source and target node.

See page here.

  

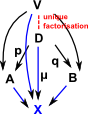
Universal Morphism

"The notion of a universal morphism to a particular colimit, or from a limit, can be expressed in terms of a comma category. Essentially, we create a category whose objects are cones, and where the limiting cone is a terminal object; then, each universal morphism for the limit is just the morphism to the terminal object. "- academickids.com

See page here.

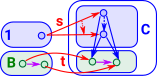 comma cone diagram

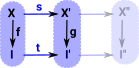
Adjunction

"Lawvere showed that the functors F : C->D and G : D->C are adjoint if and only if the comma categories FoverD and CoverG are isomorphic, and equivalent elements in the comma category can be projected onto the same element of C×D. This allows adjunctions to be described without involving sets, and was in fact the original motivation for introducing comma categories."- academickids.com

See page here.

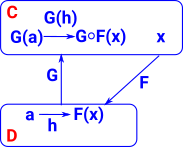 comma adjoint diagram

Kan Extension

See page here.

 

Discussion

comma category The comma category is a specialisation of the arrow category where the codomain is the same for all objects.
  Alternatively there is also a cocomma category where the domain is the same for all objects.
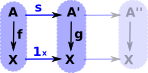comma category The above diagram could be rewritten with the X shown in each object to make it look more like the arrow category.

The concept of a comma category is related to the idea of a fibre and sheaf, reading these pages for may help with intuition.

 

Then the comma category CoverX has,

The co-comma category XoverC has,

Objects
pairs(A,f)

Where:

  • 'A' is any object in C
  • 'f' is a mapping from A to X:
A  
over f
X  
pairs(A,f)
X  
over f
A  

Morphisms
The morphism f:
  s  
(A,f) -> (A',f')
Such that the diagram commutes		 slice category
The morphism f:
  t  
(A,f) -> (A',f')
Such that the diagram commutes		 coslice category

Terminal Objects in Comma

Initial Objects in Co-Comma

If C has a terminal object '1' exists then:

C/1 = C

If C has an initial object '0' exists then:

0/C = C

Products in Comma

CoProducts in Co-Comma

In terms of the above 'pairs' we can construct a product:
Take arbitrary elements:
A,B,D
and mappings of these to X
s : A->X, t : B->X,
μ : D->X		 slice product

We can reduce the above diagram to:
slice product

 

General Comma Category

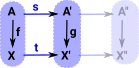comma category The comma category can be generalised further by making the target also a functor.

Further Genralisation

So we fix f: C->D and X∈D

Then the slice category C/X has,

The coslice category X/C has,

Objects
pairs(c∈C,p:Fc->X)
Fc  
over P
X  
Where
pairs(c∈C,p:X->Fc)
X  
over P
Fc  

Morphisms
The morphism f: c->c'∈C
Such that the diagram commutes		 comma category
The morphism f: c->c'∈C
Such that the diagram commutes		 co comma category

We can generalise this further by not fixing X

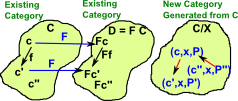
overview comma category

Instead x is combined with the pair to give a triple.

Then the comma category FoverX has,

The co-comma category FoverC has,

Objects
triple(c∈C,x∈D,p)

Where:

  • x is any element in D (no longer fixed)
Fc  
over P
X  
triple(c∈C,x∈D,p)
X  
over P
Fc  

Morphisms
The morphisms are:
f: c->c'∈C
g: x->x'∈D
Such that the diagram commutes		 comma category 2
 

Further generalisation, we add a third category 'E' like this:

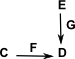
comma category 3

Then the comma category FoverX has,

The co-comma category FoverC has,

Objects
quad(c∈C,e∈E,FoverX,p)
Fc  
over P
X  
Where x is any element in D (no longer fixed) 		 

Morphisms
The morphisms are:
f: c->c'∈C
g: x->x'∈D
Such that the diagram commutes		 comma category 2
 

Comma Category References

metadata block
see also:
Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.
flag flag flag flag flag flag The Princeton Companion to Mathematics - This is a big book that attempts to give a wide overview of the whole of mathematics, inevitably there are many things missing, but it gives a good insight into the history, concepts, branches, theorems and wider perspective of mathematics. It is well written and, if you are interested in maths, this is the type of book where you can open a page at random and find something interesting to read. To some extent it can be used as a reference book, although it doesn't have tables of formula for trig functions and so on, but where it is most useful is when you want to read about various topics to find out which topics are interesting and relevant to you.

 

Terminology and Notation

Specific to this page here:

 

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2024 Martin John Baker - All rights reserved - privacy policy.