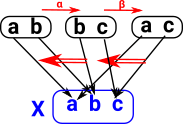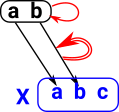Slice category is a specific case of comma category.
Slice Category
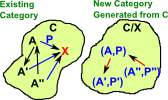
Given a category C we can 'slice' it over some object X
C which we fix in C.
| This construction allows us to start with one category 'C' and generate a different category 'C/X' by fixing a given element 'X' in C. The elements in C/X are pairs (A,P) where AC and P is a morphism from A to X. |
 |
Slice Category Examples
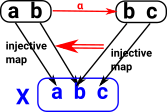
Colouring of labeled set. Here we choose as our fixed object 'X' the 3 element set containing R, G and B (for red green and blue). Every object (in this case set) has an arrow (function) to this set so all the elements are assigned a colour. When we add functions between these set objects these functions must now commute. This restricts us to functions which only map R to R, G to G and B to B. This effectively partitions the structure into 3 separate sets, one for each colour. This seems similar to fibrations. Strictly its only a fibration if the category supports pullbacks. See nlab for explanation of this.
|
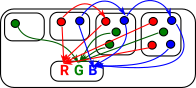 In category theory we are not really supposed to look inside objects or arrows, but we do so here to attempt to give some intuition. |
Adding a distinguished point (the origin) to Euclidean space to give a vector space. |
 |
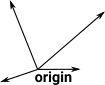'co-slice' is the dual concept, reverse all the arrows.
Comma Category References
- TheCatsters - Youtube - Slice categories 1 Nov 2008
- TheCatsters - Youtube - comma categories 2
- Wiki
- nlab
