 |
A sum in category theory is a kind of colimit. It is dual to a product discussed on the page here. It consists of the sum A+B with two arrows into it, one from A and the other from B. It must have a universal property which is: For any other object Z with maps from A and B there must be a unique arrow from A+B to Z. |
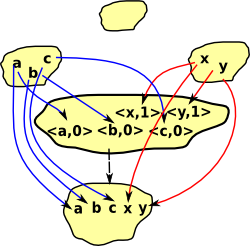
Sum Example in Set
 |
In this diagram the two sets A and B are shown with elements. Some of the elements in A+B have inputs from A, some from B and some from both. So A+B is a (not necessarily disjoint) union. So to comply with the universal property the maps into Z must respect the disjointedness or otherwise of the elements. |
| I have drawn the sum like this: |  |
but when encoding the elements we may need to tag them with a 0 or 1 to know whether they come from A or B. In algebraic terms this is like: A+A = 2*A where 2 means a Boolean type |
(a,0) (b,0) (c,0) (d,0) (c,1) (d,1) (e,1) (f,1) |
Sum Example in Integers
Sum objects are discussed in this page.
 |
We can construct the Integers from 2 natural numbers, the positive numbers and the negative numbers: Z = N+N Alternatively we can construct the Integers from a natural number and a sign (+ or -): Z = 2*N I'm not sure these equations quite work at the intersection (we don't want both +0 and -0) |
In type theory we can construct the natural numbers from zero and successor N constructors where successor is a recursive function. So if we also construct the negative natural numbers from zero and predecessor can we define these higher order functions in the sum? Can we extend successor and predecessor to both work across all of Z? |
 |
Example in Directed Graph
 |
This is like the set example with arrows between the elements. Can we have arrows into and out of the intersection like this? I can't see why not but possibly not when we go on to pushout. |
Table of Results
Sum |
||
|---|---|---|
| generalisation | a kind of colimit | |
| set example |
|
disjoint union {a,b,c}+{x,y}= |
| group | free product the free product for groups is generated by the set of all letters from a similar "almost disjoint" union where no two elements from different sets are allowed to commute. |
|
| Grp (abelian) | direct sum the group generated by the "almost" disjoint union (disjoint union of all nonzero elements, together with a common zero) |
|
| vector space | direct sum | |
| poset | least upper bound join |
|
| base topological space | wedge | |
| POS |
|
least upper bounds (joins) |
| Rng | ||
| Top | disjoint unions with their disjoint union topologies | |
| Grf | ||
| category |
Sum
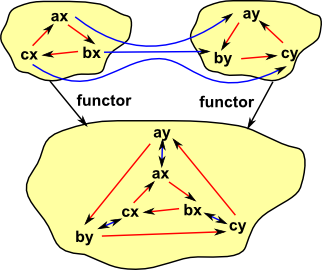
When generating a sum for objects with structure then the structure associated with the link can be added to the sum object.
Next Steps
see also:
