Maths - Category Theory - Adjunctions

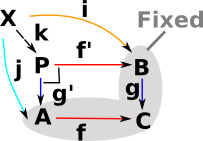
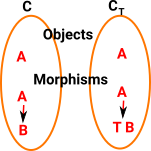
An adjunction is a looser relationship between structures than isomorphism or equivalence.

As with isomorphism and equivalence an adjunction applies to a pair of functors, F and G.

On the previous page about equivalence we looked at equivalence as an isomorphism upto isomorphism:

Isomorphism axioms

1CGF FG1D

We could look at adjunctions as a further weakening so that, instead of 2 isomorphisms of mappings we just have 2 mappings of mappings (natural transformations):

Adjunction natural transformations: note: these are not the axioms.	unit: μ : 1c => GF co-unit: ξ : FG => 1d
Adjunction axioms:	FFGF GFGG

This can intuitively make sense, for instance, if G looses information (is forgetful) then we may be able to choose a F such that: applying FG after G looses no more information than we have already lost doing G once. So going round the loop looses no more information than we have already lost.

The topic of adjunctions is a very powerful concept but can be difficult to understand, it might therefore help to approach the subject from different directions. We give two definitions and show that they are the same.

Natural Transformations

My interpretation of these natural transformations would be:

FG => 1d	For every F there is one or more G that makes FG map to identity.
1c => GF	For every F there is one or more G that makes GF a valid mapping (not necessarily identity).
1C= GF	For every F there is a G that makes FG map to identity.

Definition 1

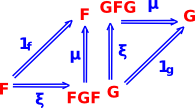An adjunction is given by a pair of functors, F and G (see diagram above) equipped with natural transformations unit: μ : 1c =>GF co-unit: ξ : FG => 1d such that the diagrams on the left (known as the triangle identities) commutes.

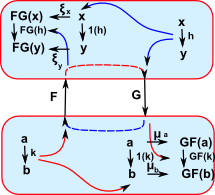We can look at this in terms of the components. At first it may appear that we cannot use natural transformations because the arrows between C and D go in opposite directions and therefore the domains and codomains are not the same. However we can rearrange the diagram so that a natural transformation goes between 1 and GF and another one goes between FG and 1. This (perhaps over-complicated) diagram is trying to represent the natuality squares of the two natural transformations and how they all link together..

For adjunctions there is a arrow in both directions between the two objects. It is not necessary that GF and FG are the identity elements but only that they have natural transformations to/from the identity elements.

FG is unit (does not change object - injective followed by surjective) but GF does change object (surjective followed by injective). Like equivalence but in one direction.

The above diagrams can also be represented as 2-cells:

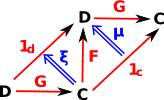Definition 2

In this approach we are still using isomorphisms between morphisms but in an apparently different way that turns out to be the same.

We have an isomorphism between a morphism in C and a morphism in D. Until now, to compare morphisms, we have used natural transformations. But natural transformations can only compare morphisms with the same domain and codomain here the morphisms, being compared, are not even in the same category.

This comparison is called a 'natural isomorphism' as follows:

We have arrows in C which are isomorphic to arrows in D. Shown here as red arrows.
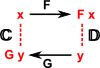	An adjunction is given by a natural isomorphism morphisms in D   morphisms in C           φ: D( F x , y ) -> C( x , G y ) for every xC and yD which is naturally isomorphic in both x and y

What are the functors that are naturally isomorphic?

Cop-> set   D(F _,y)   x D(F x,y)	Cop-> set   C(_,G y)   x C(x,G y)
D-> set   D(F x,_)   y D(F x,y)	D-> set   C(x,G _)   y C(x,G y)

So the naturality square in x is:

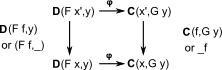We precompose with F f to get: fx -> fx' -> y

Adjunctions and Monads

Every adjunction gives rise to a monad. Every monad gives rise to many adjunctions

E-M Adjunction from Monad

Kl Adjunction from Monad

As String Diagrams

String diagrams are the Poincaré dual of the usual category theoretic diagrams, they can be useful for 2-categories such as adjunctions. (more about string diagrams on this page).

	Category Diagram	String Diagram
We start with a diagram like this (F is left adjoint to G) and add 2 natural transformations below (η and ξ) with the following axioms.
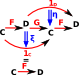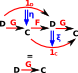We take this diagram: between functors and put it in a diagram with the objects. The string diagram has the identity functor omitted as explained above. Also, for simplicity, ξ is not shown in a circle.
And again for η.
Now for the triangle equalities. In the string diagram it just looks like we can pull the line straight.
The other triangle equality

 

Examples

Some very General Adjunctions

existential,sum Σ		weakening (adding an extra assumption)
weakening		universal, product Π
equality		contraction
truth		comprehension or subset types
equality		comprehension
quotients		equality

Links to More Detailed Examples

• Monoid - see this page
• Preorder - see this page
• Graphs

Category of graphs described on page here.

Between reflexive graph and set. In reflexive graph: every node has loop to itself.

Between irreflexive graph and set. In irreflexive graph: every node does not have loop to itself.

Between dynamical system graph and set. In dynamical system graph: every node has one outgoing arrow.

Different dynamical system graph and set. This time the morphism to set defines the fixpoints.

Adjoint Pairs

The basis on a vector space

The free group on a set

G G / [G,G] commutator subgroup

universal enveloping algebra of a Lie algebra

completion of a metric space

EuclideanSpace

home

Prerequisites

We need to know about category theory concepts described on these pages and, in particular, natural transformations.

Set Symbols

Category Theory