See these Wiki articles:
Galois connection
Let (A, ≤) and (B, ≤) be two partially ordered sets. A monotone Galois connection between these posets consists of two monotone functions:
such that for all a in A and b in B, we have F(a) ≤ b if and only if a ≤ G(b). |
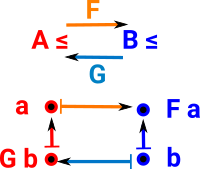 |
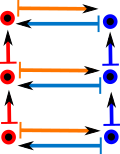
This works for composed morphisms like this: (if we work through each rectangle the above condition holds) |
 |
| The posets don't have to be isomorphic, morphisms in A can converge to points in B for example: | 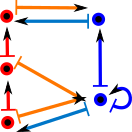 |
| However the morphism F has to be continuous (in some sort of topological sense), that is, we can't have sort of tears like this: | 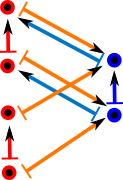 |
Preordered Set
Here we work in the category of preordered sets (I have illustrated this as a directed graph, I find it helpful to use draw directed graphs as described in the box on the right)
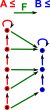 |
Here we look at a perordered set ≤(red) and a mapping to another perordered set (blue). The morphism between them (green) preserves the ordering. That is: if a ≤ a' then F(a) ≤ F(a') |
| So is there a mapping (G) back from B to A that preserves as much structure as possible in some unique way? | |
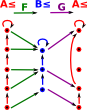 |
Here is a first attempt, as we can see we can compose these morphisms and still preserve the order structure |
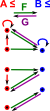 |
So lets add another condition: GF(a) ≤ a This condition is not met for our first choice of G (on the diagram on the left this is interpreted as reversing one of the red arrows). |
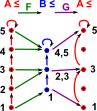 |
However, given the morphism F then there is a way to choose a way to choose the morphism G so that the order is preserved relative to the original sequence. For instance, if the number the elements of 'A' with ascending values. We then map these values onto 'B' using the morphism 'F'. We can then determine G by mapping the highest value for each element in 'B' to the corresponding number in 'A'. G is then the adjoint of F. |
So, for adjoint morphisms: F(a) ≤ b if and only if a ≤ G(b) Now we have a unique mapping G we can go on to show the unit and co-unit: |
|
 |
μ : 1c =>GF So the unit maps 1c to GF as in this diagram. In this diagram we can't derive mappings from movement of points, we just map the mappings directly. I added in the purple arrows to make it into a graph, they are not really generated by GF. |
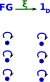 |
ξ : FG => 1d In this case the co-unit is trivial. |
Same Thing Using Definition 2
In this case we take an element 'A' of C and an element 'X' of D. We can then determine GX and FA by following the arrows. The arrow A->GX is then isomorphic to the arrow FA->X. This must be so for any 'A' in C and 'X' in D. |
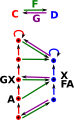 |
Poset
An endofunctor on posets models closure. Posets don't have loops, therefore defined by fixpoints.
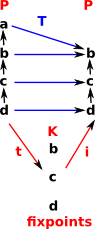 |
Define T: P -> P with
gives T² <= T (that is it is idempotent) |
 |
Which gives an adjunction: t![]() i
i
This is discussed as a monad on page here.
Implementing Posets in FriCas program is discussed on page here.
| Category | ||
|---|---|---|
| type theory | quantifiers | substitution (Cartesian maps) |