| Imagine we have a property (a predicate) P that is true for all values of x |  |
| We can substitute y for x where y is a function of x: |  |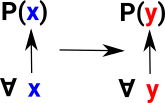
 |
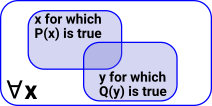- The universal quantifier is the right adjoint of substitution.
- The existential quantifier is the left adjoint of substitution.
Πx:T -->
<-- (-)×T
Σx:T -->
As a sort of intuitive justification for this:
If we have a total function:
f: x -> y
Then we are saying 'y' exists for all 'x'.
https://ncatlab.org/nlab/show/substitution
Substitute Variables and Literals
In type theory the deconstruct + construct (compute) allows us to substitute one variable for another.
Can we substitute between variables and literal values?
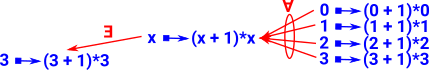
If we start with a variable we can always go to a literal value (
) but all literal values must apply (
) before we can convert to a variable.
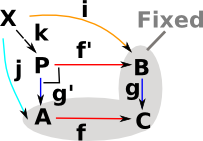
The following diagram is my attempt to draw this as fibre bundles:
See Bartosz Milewski on his blog here.
| existential,sum Σ |
 |
weakening |
| weakening | |
universal, product Π |
Substitute Variables and Expressions (Terms)
We have seen interesting structure when we substitute between variables and literals, now lets try substituting between variables and expressions.
In Type Theory
Use 'context extension' instead of substitution.
https://ncatlab.org/nlab/show/context+extension
In Category Theory
Pullback
Substitution of a term into a predicate is pullback, but substitution of a term into a term is composition. Or if you are a type theorist: Substitution of a term into a dependent type is pullback, but substitution of a term into a term is composition. |
 |
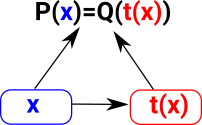Discussed more on these pages:
- More about binding variables and substitution on the type theory pages.
- More about substitution and lambda functions on the page here .
Pullback Terminology
As often happens in mathematics the term 'pullback' is overloaded. There are different definitions, as precomposition or as a Cartesian square. These definitions can sometimes coincide as a pullback bundle.
Pullback as Precomposition
Here the points map from left to right but some property or mathematical structure goes back in the other direction.
As a simple example in set. We take a subset of B which are the elements which have some property P which is defined by a map from B to P.We then precompose this with a map t : A->B this then defines a subset of A. This is substitution as it allows us to substitute A for B. The points map from A to B but we have transferred the property from B to A.
- More about substitution and equality on this page.
- Using substitution in proofs on this page.
- Substitution and adjunction discussed on this page.
- Pullback and equality discussed on this page.
Pullback as a Cartesian Square
This definition is the limit of the diagram:
A -> C <- B
It has a universal property that the cone from P is the most general, arrows from any other object X factor through it.
See page here.
Pullback Bundle
In many cases the two definitions above coincide. We can consider this as a product with the additional condition that the square commutes.
