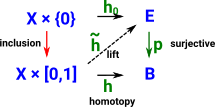Introduction
This page continues from the model category page which is introduced on the page here.
Fibrations have additional structure to fiber bundles (see the page about fiber bundles here) which allows some structure in B to be 'lifted' to E. (see Wikipedia page).
Fibration and Co-fibration
Homotopy has the concept of:
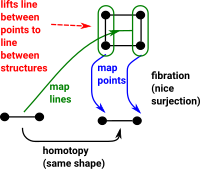
- a fibration which has the lifting property.
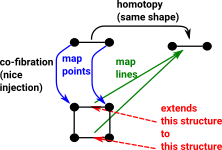
- a co-fibration which has the extension property -extension is dual to lift.
Fibration |
Co-fibration (Extension Property) |
|
|---|---|---|
| Homotopy | Fibration |
Co-fibration (see page here) |
Combinatorics |
Kan fibration (see page here) |
Kan extension (see page here) |
Kan fibrations are combinatorial analogs of Serre fibrations of topological spaces.
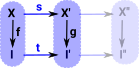
Lifting Property in Topology
This fibration is like a fibre bundle in sets, the differences are:
That is: the fibration goes from E to B (the vertices map in that direction) but the open sets map in the other direction so if we first map each point to an open set containing only that point we can then map to E. So composing these arrows gives 'lift'. |
 |
For more about the lifting property see the page here.
Fibration - Line to Point Map Example
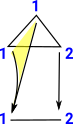
| To keep things simple, take the example of a line continuously retracted down to a point. |  |
 |
To see this, in its most general form, as a continuous map between topological spaces I have drawn the line consisting of representative points and open sets. |
For it to be a continuous map the preimage of an open set must be an open set. We don't want to have to make any arbitrary decisions about which open set to map back to, so the preimage is the open set around the whole line. |
 The red arrow is a map between open sets. |
This is the homotopy lifting property. When we look at more complicated examples (see fibration page) we will see structure between points being lifted to structure between open sets.
Coding Fibrations as Simplicial Sets
So how can we model fibrations like this using simplicial sets? Lets look again at the example where two circles that touch at a point can be continuously deformed into a circle with a line through the middle.
Here is an attempt to code as a simplicial set. The deformation into a circle with a line through the middle is done by a degenerate map which creates two instances of point b. Note: the two degenerate points b must always have maps between each other. |
 |
As Continuous Map
 |
Here we are looking for a continuous map to map a topological space to map to something homotopy equivalent. As explained on page here a function f : X->Y is continuous if f-1(V) is open for every open set V in Y. Can we treat simplcies like open sets? So the simplcies map in the opposite direction to vertices? The simplcies may map to simplcies of a different dimension, so here the middle vertex maps to a bar (edge). This continuous map should preserve loops, does this do that? can we prove it? |
At Higher Level
 |
What rules follow from having degenerate points in the simplicial set? For example from this diagram here: |
| We can join the two b points on the left and fill in the triangle of b's. |  |
For more information see these pages:
Fibration and Lifting in Simplicial Sets
 |
Here 1 and 2 are points in a simplicial set. In E there are degenerate lines {1,1} and {2,2}. The lifting property allows us to transfer structure on the points (such as a map between them) to the same structure on the lines. |
 |
This works with higher dimensions. Here two degenerate points in the triangle collapse down to to a point on the line. |
Fibrations and Indexing
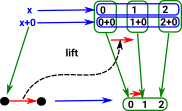
In sets we can look at fibrations as an 'I' indexed family of sets. To denote this I have replaced B with the indexing set 'I' and replaced E with the family of sets X, like this: 
In the slice category of sets:
|
These are the objects |
 |
These are the arrows |
That is, in the slice category the indexing set remains the same.
Here are some examples of comma categories. In these cases all the objects are in the same category (including the fixed object). The comma category generalises this by allowing the objects to come from other categories.
Arrow categorysee page here |
 |
|
Examples |
Slice categorysee page here |
 |
|
|
Co-slice categorysee page here |
 |
|
Examples |
Fibrations and Substitutions
Substitution as Pullback
Can we express substitution in category theory terms? See discussion on page here.
| Substitution of a term into a predicate is pullback, but substitution of a term into a term is composition. | |
| Type theory version | Substitution of a term into a dependant type is pullback, but substitution of a term into a term is composition. |
There is a discussion of this topic on this site.
Say we have two propositions, say:
- y = 2*x+1
- z = w + 3
Then, under certain conditions, we could substitute a variable for a term. Say, let w=y so:
- z = (2*x+1) + 3
 |
So here we draw this substitution as a pullback.
|
Fibrations and Lifting
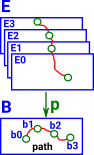
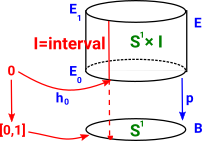
Given a path [0,1] in the base space B and a point e0 in the total space E. We can 'lift' this path into the total space E as a path starting at e0. |
 |
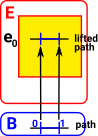Here I am mostly concentrating on discrete structures so we need a looser concept of continuous mappings. |
 |
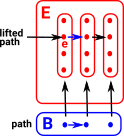An inclusion from [0,1] into B can be lifted into E: If we are using CW-complexes to model our topological spaces then we can use a slightly weaker form of fibration known as a Serre fibration. |
 |
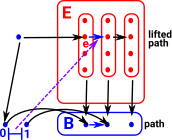Simple ExampleFibration and co-fibration is related to fibre bundles as discussed on the page here. To recap from this page we can start with a surjective mapping between sets and then add extra structure to these sets. In this example we have two sets B the base set and E the total set and a surjective mapping p between them. |
 |
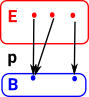| We get a fibre bundle by trying to get as close as we can to the inverse of the function p without making arbitrary choices. |  |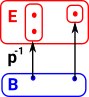
On this page want to expand the idea of fibre bundles on sets to add more structure. As an example lets go from sets to directed graphs. The function p must now map the arrows as well as the vertices. |
 |
What is the closest we can get to an inverse function? Here is a possibility. This 'lifts' the vertices to sets which may contain multiple vertices. |
 |
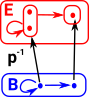Is this valid because two paths join and this is like a tear which is not allowed in topology/homotopy transforms? |
 |
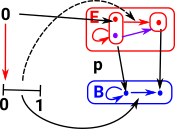So E is like a product. Here we lift the interval to the red arrow in E. note: we think of this as being continuous even though this example has discrete vertices. |
 |
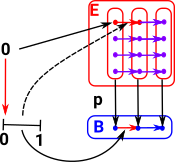But E only needs to be like a product locally. |
 |
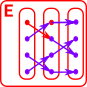Can we think of this lifted mapping as being between the sets? |
 |
Fibrations and Proof
As an example lets invent an algebra and try to prove, in this algebra, that x=x+0.
In this algebra there are 3 elements 0, 1 and 2. Then there is one operation +.
 |
So given that 0=0+0 , 1=1+0 and 2=2+0 then we want to prove that x=x+0. That is, given some property that is true for every element we want to prove that it is true for the set as a whole. |
More information on these pages:
- Fibrations
- Proof of Equality
- Writing code for implementing algebras on this page
Fibration
We can generalise a fibre bundle to have more structure than a type indexed by a set:
- A fibration allows us to use something more complicated than a set to index types.
- A sheaf allows us to relate local and global structure.
FibrationIn this diagram B represents the base space and E represents the total space. B is now more than the index set because it now has structure. p is a projection of the total space into the base space. |
 |
|
 |
The diagram needs to have the lifting property which says that there must be an arrow h~ from the path to E. So given the structure in E0 we can get the structure at other points. |
|
Fibration ExampleA cylinder (S1*I) mapped onto a circle (S1). This map is a projection locally (upto homeomorphism). Since we only require a projection locally we could also project from a helix or a Möbius band. |
 |
|
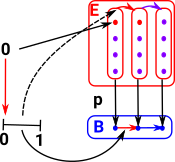Fibrations of Graphs
theory: topological graph theory
| undirected graph: | covering projection |
| directed graph: | fibration (weaker form of covering projection) |
Here is an example for directed multigraphs. Each node in the top graph maps to the bottom graph (fibration). The corresponding node always has the same number and colour of incoming arcs (but not necessarily outgoing arcs). This gives some sort of local invariance. |
 |
Fibration and Co-fibration
Homotopy has the concept of:
- a fibration which has the lifting property.
- a co-fibration which has the extension property -extension is dual to lift.
Fibration |
Co-fibration (Extension Property) |
|
|---|---|---|
| Homotopy | Fibration |
Co-fibration (see page here) |
Combinatorics |
Kan fibration (see page here) |
Kan extension (see page here) |
Kan fibrations are combinatorial analogs of Serre fibrations of topological spaces.
Next
If we reverse the arrows in the diagram for fibrations we get the diagram for cofobrations:
Co-fibration involves the concept of extension
- fibration - lift
- co-fibration - extension
Extension is dual to lift.
- Fibrations and Cofibrations are used in model theory.
