It is useful, for certain types of reasoning, to have the things we know about a situation in the form of implications. For instance:
| A -> B | A implies B |
of even:
| A /\ B /\ C -> D | A and B and C implies D |
Deduction Using Implies
So if the following are true:
then we can deduce: A -> D for example, by combining the implications (substituting). |
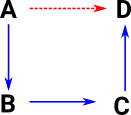 |
Forward and Backward Chaining
Diagrams, such as the one above, give us a graphical guide.
As Meet and Join
We may need to express the implication in terms of meet and join ('or' and 'and') . To see how to do this lets look at a truth table for it:
| A | B | A->B |
| F | F | T |
| F | T | T |
| T | F | F |
| T | T | T |
Note: I've drawn the truth table as Boolean values but we can use constructive logic instead (law of excluded middle not required).
