Intuitionistic logic sounds like a contradiction in terms, this is we think of intuition as being the opposite of logic. An alternative name is 'constructive logic' and perhaps this better describes the nature of this form of logic.
In intuitionistic logic a statement is true only if it is proven to be true and it is false only if it is proven to be false, so for instance we can't imply something is true just because it is not false. In other words we do not use the law of the excluded middle.
This is the way that we construct information in the everyday world and it is the basis of mathematical constructivism.
Heyting Algebra
Unlike boolean algebra we do not have 'not' operation, instead we have a 'pseudo complement'.
| Boolean |  |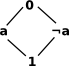
A Boolean algebra is a full lattice where a \/ ¬a is 1 (true) |
| Heyting |  |
This does not apply for Heyting algebra, that is no: 'Law of excluded middle' |
We do have a \/ operation but it does not have the property that: a \/ ¬a = 1.
A Heyting lattice (pseudo boolean lattice) is a relativly complemented lattice.
We can express Heyting algebra properties in terms of this pseudo complement or, alternativly, we can express Heyting algebra properties using the 'implication operation
'->'. Where:
x -> b is the largest element whose intersection with x is contained in b.
| a ^ x ≤ b | b is pseudo complement of a relative to x |
| a < (x -> b) | Equivalently this can be expressed in terms of the 'implication operation |
So a Heyting algebra is a lattice with a binary operation x->y satisfying the double-horn sentence:
a < (x -> b) iff a ^ x ≤ b
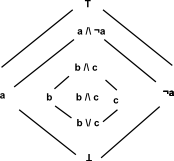
Example: 'A' is pseudo complement of 'BC' relative to 'ABC'
A ^ BC ≤ ABC where:
|
 |
I have drawn this diagram so we can get the 'pseudo complement' relative to A^B^C by reflecting in the red line. |
| x | y | x /\ y | x \/ y | x -> y |
|---|---|---|---|---|
| ø | ø | ø | ø | ø |
| A | ø | ø | A | ø |
| B | ø | ø | B | ø |
| A/\B | ø | ø | A/\B | ø |
| ø | A | ø | ø | ø |
| A | A | A | A | A |
| B | A | ø | A/\B | ø |
| A/\B | A | A | A/\B | ø |
| ø | B | ø | B | ø |
| A | B | ø | A/\B | ø |
| B | B | B | B | B |
| A/\B | B | B | A/\B | ø |
| ø | A/\B | ø | A/\B | ø |
| A | A/\B | A | A/\B | A |
| B | A/\B | B | A/\B | B |
| A/\B | A/\B | A/\B | A/\B | A/\B |
BHK Interpretation
Where BHK is 'Brouwer, Heyting, Kolmogorov'
- (H1) A /\ B means A and B, that is, a proof of A /\ B is given by a proof of A and a proof of B.
- (H2) A \/ B means A or B, that is, a proof of A \/ B is given by either a proof of A or a proof of B.
- (H3) A -> B means that if A is true then B is also, that is, a proof of A -> B is a construction which permits us to transform any proof of A into a proof of B.
- (H4) Absurdity _|_ (contradiction) has no proof; a proof of A is a construction which transforms any hypothetical proof of A into a proof of a contradiction.
- (H5) A proof of
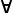xA(x) is a construction which transforms a proof of d
D (D the intended range of the variable x) into a proof of A(d). - (H6) A proof of
xA(x) is given by providing dD, and a proof of A(d).
Heyting's formalization
For logical connectives p & q:
- A mathematical proposition p always demands a mathematical construction with certain given properties; it can be asserted as soon as such a construction has been carried out.
- p /\ q can be asserted if and only if both p and q can be asserted.
- p \/ q can be asserted if and only if at least one of the propositions p and q can be asserted.
- p can be asserted if and only if we possess a construction which from the supposition that a construction p were carried out, leads to a contradiction.
- The implication p -> q can be asserted, if and only if we possess a construction r, which, joined to any construction proving p (supposing that the latter be effected), would automatically effect a construction proving q.
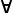- |- (x)p(x) means that p(x) is true for every x in Q [over which x ranges]; in other words, we possess a general method of construction which, if any element a of Q is chosen, yields by specialization the construction p(a).
- (x)p(x) will be true if and only if an element a of Q for which p(a) is true has actually been constructed.
The language 
has:
- predicate letters P, Q(.),? of all arities and individual variables a, b, c,? (with or without subscripts 1,2,?)
- symbols &, \/, ->, ,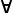,for the logical connectives and quantifiers, and parentheses (, ).
- prime formulas of are expressions such as P, Q(a), R(a, b, a) where P, Q(.), R(?) are 0-ary, 1-ary and 3-ary predicate letters respectively; that is, the result of filling each blank in a predicate letter by an individual variable symbol is a prime formula.
The (well-formed) formulas of are defined inductively as follows.
- Each prime formula is a formula.
- If A and B are formulas, so are (A & B), (A \/ B), (A -> B) and A.
- If A is a formula and x is a variable, thenxA andxA are formulas.
In general, we use
A, B, C as metavariables for well-formed formulas
x, y, z as metavariables for individual variables.
Anticipating applications (for example to intuitionistic arithmetic) we use s, t as metavariables for terms; in the case of pure predicate logic, terms are simply individual variables.
An occurrence of a variable x in a formula A is bound if it is within the scope of a quantifierx orx, otherwise free. Intuitionistically as classically, "(A <-> B)" abbreviates "(A -> B) & (B -> A)," and parentheses are omitted when this causes no confusion.
A |- B means that B follows from A
A might be treated as negation or it might be treated as an abbreviation for (A -> _|_)
_|_ = false
T = true
Axioms
- a -> (a /\ a)
- (a /\ b) -> (b /\ a)
- (a -> b) -> ((a /\ c)-> (b /\ c))
- ((a -> b) /\ (b -> c)) -> (a -> c)
- b -> (a -> b)
- (a /\ (a -> b)) -> b
- a -> (a \/ b)
- (a \/ b) -> (b \/ a)
- ((a -> c) /\ (b -> c)) -> ((a \/ b) -> c)
- a -> (a -> b)
- ((a -> b) /\ (a -> b)) -> a
Rules of Inference
There are three rules of inference:
- Modus Ponens: From A and (A -> B), conclude B.
- -Introduction: From (C -> A(x)), where x is a variable which does not occur free in C, conclude (C ->xA(x)).
- -Elimination: From (A(x) -> C), where x is a variable which does not occur free in C, conclude (xA(x) -> C).
Fomulas
- then1: A -> (B -> A)
- then2: (A -> B) -> ((A -> (B -> C)) -> (A -> C))
- and1: A & B -> A
- and2: A & B -> B
- and3: A -> (B -> A & B)
- or1: A -> A \/ B
- or2: B -> A \/ B
- or3: (A -> C) -> ((B -> C) -> (A \/ B -> C))
- (A -> B) -> ((A -> B) -> A)
- A -> (A -> B)
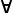- xA(x) -> A(t)
- A(t) ->xA(x)
