Maths - Sequent Calculus

In sequent calculus the notation for judgments is extended to have the following form:

antecedent or context sequence of formulas considered conjunctively - all assumed to be true	turnstile symbol	succedent sequence of formulas considered disjunctively - at least one is true
A1,A2,A3...An		B1,B2,B3...Bn

This means that whenever every A_i is true then at least one B_i is true.

Where:

• A and B are formulae of first-order predicate logic (can also restrict this to propositional logic),
• Γ, Δ, Σ, and Π are finite, possibly empty, sequences of formulae called contexts. The order of formulae do not matter.

Combining Rules

ΓΔ   ΣΠ Γ,ΣΔ, Π We can combine the above two rules to give the rule below the line.

ΓA   AΠ ΓΠ If the antecedent of one rule is the same as the succedent of another rule it is possible to chain the rules together, cancelling out the common term. This is a special case of the cut rule below.

Arguments, proofs or derivations in this language.

Identity Axiom Rule

'A' a given term is assumed to be true. So A implies itself. This has the role of the identity.

AA (I)

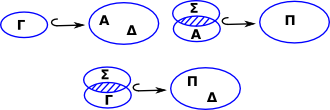
Cut Rule

ΓΔ, A   A, ΣΠ Γ,ΣΔ, Π (Cut)

This rule allows us to eliminate A from the result.

Can we interpret this in terms of subsets?

/\ Rules

Here are the rules for conjunction (and). Some versions of the introduction rule don't include Δ and Π.

Elimination		Introduction
Γ,AΔ Γ,A/\BΔ (/\L1)	Γ,BΔ Γ,A/\BΔ (/\L2)	ΓA,Δ   ΣB,Π Γ,ΣΔ,Π,A/\B (\/R)

As an example of how to interpret /\L1 it means whenever we can prove that Δ can be concluded from some sequence of formulae that contain A, then one can also conclude Δ from the stronger assumption, that A/\B holds. When Γ,A/\B is on the left side then it is equivalent to Γ,A,B so the rule is just saying that we can just add an arbitary B to the left hand side which is one of the weakening rules below.

Here is an attempt to represent L1 in terms of subsets. This seems to work fine in these terms. that is if the intersection of Γ and A is a subset of Δ. then the intersection of Γ and A/\B must be a (possibly smaller) subset of Δ.

\/ Rules

Here are the rules for disjunction (or).

Elimination	Introduction
Γ,AΔ   Σ,BΠ Γ,Σ,A\/BΔ,Π (\/L)	ΓA,Δ ΓΔ,A\/B (\/R1)	ΓB,Δ ΓΔ,A\/B \/R2)

-> Rules

Here are the rules for implication.

Elimination	Introduction
ΓA,Δ   Σ,BΠ Γ,Σ,A->BΔ,Π (->L) Modus ponens	Γ,AB,Δ ΓA->B,Δ (->R) Conditional proof

¬ Rules

Left	Right
ΓA,Δ Γ,¬AΔ (¬L)	Γ,AΔ Γ¬A,Δ (¬R)

The rule (¬R) states that, if Γ and A suffice to conclude Δ, then from Γ alone one can either still conclude Δ or A must be false(¬A holds).

Note: no rules which imply excluded middle?

Rules

For universal quantifier we will use the notationx:σ.A(x) which is true if A(x) is true for every 'x' in type 'σ', where:

• is start of this universal quantifier syntax.
• x is a variable which ranges over given type.
• : means 'has type'.
• σ indicates the type.
• . seperator.
• A(x) is a predicate that is a function of x.

For an intuition about the quantifier rules, consider the rule (R). We cannot conclude thatx A holds just from A[y/x]. If, however, the variable y is not mentioned elsewhere (i.e. it can still be chosen freely, without influencing the other formulae), then one may assume, that A[y/x] holds for any value of y.

• t denotes an arbitrary term,
• x and y denote variables,
• A[t/x] means that A is a function of x where x is a free variable. By substituting the term t for every free occurrence of the variable x in formula A.

Elimination	Introduction
Γ,A[t/x]Δ Γ,xAΔ (L)	ΓA[y/x],Δ ΓxA,Δ (R)

The variable y must not occur free within Γ and Δ. Alternatively, the variable y must not appear anywhere in the respective lower sequents.

In terms of subsets. Since x is a free element of the set

Rules

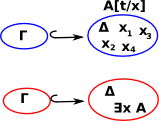
For existential quantifier we will use the notationx:σ.A(x)

• t denotes an arbitrary term,
• x and y denote variables,
• A[t/x] denotes the formula that is obtained by substituting the term t for every free occurrence of the variable x in formula A, a variable is said to occur free within a formula if it occurs outside the scope of quantifiersor

Elimination	Introduction
Γ,A[y/x]Δ Γ,xAΔ (L)	ΓA[t/x],Δ ΓxA,Δ (R)

The variable y must not occur free within Γ and Δ. Alternatively, the variable y must not appear anywhere in the respective lower sequents.

Can we interpret this in terms of subsets?

Weakening Rules

Weakening (W) allows the addition of arbitrary elements to a sequence. This is allowed:

• In the antecedent because we can always restrict the scope of our proof
• In the succedent because we can always allow for alternative conclusions.

Elimination	Introduction
ΓΔ Γ,AΔ (WL)	ΓΔ ΓA,Δ (WR)

Here is an attempt to represent weakening in terms of subsets. Adding 'A' to the antecedent makes it smaller and adding 'A' to the succedent makes it larger, both of which preserve the subset relationship.

Contraction Rules

Idempotence of conjunction and disjunction.

As with sets, neither the order nor (in this case) multiples of occurrences of elements of the sequences matters.

Elimination	Introduction
Γ,A,AΔ Γ,AΔ (CL)	ΓA,A,Δ ΓA,Δ (CR)

Permutation Rules

As with sets, neither the order nor multiple of occurrences of elements of the sequences matters.

Elimination	Introduction
Γ,A,B,Σ]Δ Γ,B,A,ΣΔ (PL)	ΓΣ,A,B,Δ ΓΣ,B,A,Δ (PR)

T and _|_ Rules

If we assume false is true then any arbitary proposition is true.

True is always true and follows from anything.

Elimination	Introduction
_|_Δ   Ex falso quodlibet	ΓT   Tautology introduction

 

EuclideanSpace

home

Prerequisites

Mathematical logic or symbolic logic is related to:

• boolean algebra
• set theory

 

Logic Notation

Writing Logic Code Using a CAS Program