Maths - Predicate Logic

Predicate Logic (or also called Predicate Calculus) is the term for a formal and symbolic system of logic like first-order logic, second-order logic and so on.

It is defined over some (possibly infinite) set. It requires some form of assignment or relationship of the elements of the set to give true or false values.

Predicate Logic

From site here :

A predicate is an expression of one or more variables defined on some specific domain. A predicate with variables can be made a proposition by either assigning a value to the variable or by quantifying the variable.

The following are examples of predicates :

• Let E(x, y) denote "x = y"
• Let X(a, b, c) denote "a + b + c = 0"
• Let M(x, y) denote "x is married to y"

Examples

Examples that depend on one parameter:

isEven : Nat -> Bool
isLessThan4 : Nat -> Bool

Examples that depend on two parameters:

equals : (Nat,Nat) -> Bool Typically relations depend on two parameters.
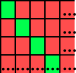evenAndLess4 : (Nat,Nat) -> Bool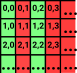

Morphisms Between Predicates

Say we have two predicates which depend on one parameter T:

T -> Bool

and we want to investigate a product of them:

( T -> Bool ) × ( T -> Bool )

In order to investigate this we can represent T -> Bool as an exponent: Bool^T so we have: Bool^T × Bool^T.

The identity: (B × C)^A = B^A × C^A works for types (up to isomorphism) so we have:

Bool^T × Bool^T = (Bool × Bool)^T

where Bool × Bool is a logic table.

So translating back from exponential notation we have:

( T -> Bool ) × ( T -> Bool ) = ( T -> Bool×Bool )

If we have an operation Bool×Bool->Bool (such as 'and' or 'or') then we have a binary operation for predicates:

( T -> Bool ) × ( T -> Bool ) = ( T -> Bool )

Note: we can generalise this from Boolean values to 'truth objects' Ω - see topos theory.

Logic Language

Terms

Constants

Values have two values ether true of false, we may use alternative names as follows:

true	1	T
false	0	_|_

Variables

A variable is a letter or symbol used to represent a value (an object, not a proposition). A predicate containing variables can be made into a valid proposition if the variables are either:

• assigned a value.
• or quantified using a quantifier.

Functions

Composite terms are formed by applying function symbols to other terms. Each function symbol has an 'arity' that is it takes in 'n' parameters and returns 'm' parameters.

Quantifiers

universal quantifier:		for all
existential quantifier:		there exists (for some)

For universal quantifier we will use the notationx:σ.A(x) which is true if A(x) is true for every 'x' in type 'σ', where:

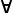• is start of this universal quantifier syntax.
• x is a variable which ranges over given type.
• : means 'has type'.
• σ indicates the type.
• . seperator.
• A(x) is a predicate that is a function of x.

So,

x:σ.A(x) = A(a) /\ A(b) /\ ...

where a:σ, b:σ ... are all objects in discourse.

Simarly for existential quantifier we will use the notationx:σ.A(x) which is true if A(x) is true for at least one 'x' in type 'σ'

x:σ.A(x) = A(a) \/ A(b) \/ ...

where a:σ, b:σ ... are all objects in discourse.

Introduction Rules

A x.A (I) x not free in A	A[t/x] x.A (I)

Elimination Rules

x.A(x) A[x/t] (E)	[A] ... x.A B B (E) x not free in B

Formulas

If x₁, … ,x_n are elements of the set and P is an n-place predicate symbol, then

P(x₁, … ,x_n) is an elementry formula

If A and B are formulas, then

• A /\ B
• A \/ B
• A ¬ B
• A ==> B
• A <=> B
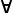• x A
• x A

are also formulas.

Connectives

Commonly used logical connectives include:

• Negation (not) ( or ~)
• Conjunction (and) (/\,wedge, &, or )
• Disjunction (or) (/\ or vee )
• Material implication (if...then) (-> or supset)
• Biconditional (if and only if) (iff) (xnor) (<-> , equiv, or = )

Programming

Formation Rules

[x:A] ... A is a type P is a type (x:A).P (F) P is a type on the assumption that x is a variable of type A	[x:A] ... A is a type P is a type (x:A).P (F) P is a type on the assumption that x is a variable of type A

Introduction Rules

[x:A] ... .p:P (λ x:A).p : (x:A).P (I) x not free in A	a:A p:P[a/x] (a,p):(x:A).P (I)

Elimination Rules

a:A f: (x:A).P f a:P[a/x] (E)	p:(x:A).P fst p:A p:(x:A).P snd p: P[fst p/x] (E) projections

Computation Rules

((λ x:A).p a -> p[a/x]	fst (p,q) -> p snd (p,q) -> q

 

EuclideanSpace

home

Prerequisites

Mathematical logic or symbolic logic is related to:

• boolean algebra
• set theory

 

Logic Notation

Writing Logic Code Using a CAS Program