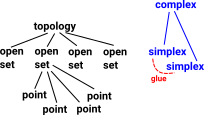
Delta Complexes

Delta Complex

When we looked at cell complexes we got a chain of 'face maps' between each dimension and the next lower one.

In homology we treat this as a chain of abelian groups (more detail on the page here).

Sometimes, rather than defining faces, of any dimension, by their vertices It is useful to define each dimention in terms of the next lower dimenstion, for example, when generating homotopy groups such as the fundamental group.

To do this we represent the complex as a sequence of 'face maps' each one indexed into the next.

Geometric Realisation and Delta Complexes

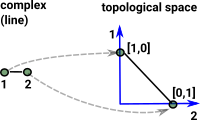
There is a close connection between geometric realisation and delta complexes.

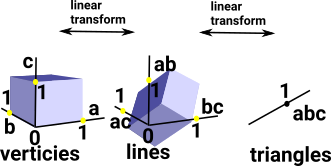
When we embed a simplicial set or cell complex into a topological space we have a dimension for each vertex and the vertex is represented by a vector from 0 to 1 in that dimension. We can do the same for lines, triangles ... There in now a linear mapping between vertices, lines, triangles... (that is a matrix). So a topological shape is now represented by a sequence of matrices.

More information:

• page about geometric realisation here
• page about delta complexes here

Implementation

The ordering of the indexes is important. The indexes of any face are always ordered acording to their order in the next order face.

As an example consider the representation for a single tetrahedron:

The usual representation would be:	(1,2,3,4)
which is very efficient but it does not allow us to refer to its edges and triangles.
Here we have indexed: The 4 vertices (in red) The 6 edges (in green) The 4 triangles (in blue)
This representation holds all these indexes so that we don't have to keep creating them and they can be used consistently.
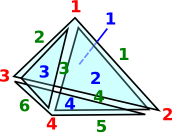
Face Maps So the tetrahedron indexes its 4 triangles, each triangle indexes its 3 edges and each edge indexes its 2 vertices. Each face table therefore indexes into the next. To show this I have drawn some of the arrows (I could not draw all the arrows as that would have made the diagram too messy).

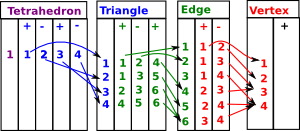Since edges, triangles, tetrahedrons, etc. are oriented we need to put the indexed in a certain order.

Edges are directed in the order of the vertex indices. That is low numbered index to high numbered index: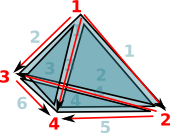
For triangles we go in the order of the edges, except the middle edge is reversed. On the diagram the edges are coloured as follows: green arrows - not reversed purple arrows - reversed This gives the triangles a consistent winding
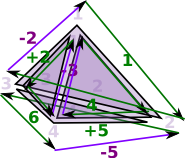However the whole tetrahedron is not yet consistent because some adjacent edges go in the same direction and some go in opposite directions.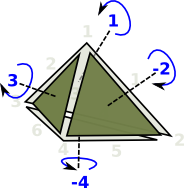
This gives the orientation of the faces as given by the right hand rule. That is: if the thumb of the right hand is outside the tetrahedion, pointing toward the face, then the fingers tend to curl round in the direction of the winding.

The higher order faces may continue on in this manor, however it is difficult to visualize.

So to represent this structure we use the following:

Rep := Record(VERTS:VS,SIMP:List(List(Integer)))

where:

• VS is a list of verticies in whatever form we are using.
• Integer is an index, a negative sign reverses the direction.
• The inner list represents one of the tables shown above, edge has 2 entries, triangle has 3, and so on.
• The outer list holds all the tables, edge first, then triangles and so on.

Example

Here is an example of a tetrahedron (2-sphere).

(1) -> DELTA := DeltaComplex(VertexSetAbstract)
 

   (1)  DeltaComplex(VertexSetAbstract)
                                                                   Type: Type
(2) -> b4 := sphereSolid(3)$SimplicialComplexFactory
 

   (2)  [1  2  3  4]
                             Type: FiniteSimplicialComplex(VertexSetAbstract)
(3) -> c4 := deltaComplex(b4)
 

   (3)
   edge:[[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]] triangle:
     [[1,2,4],[1,3,5],[2,3,6],[4,5,6]]
      tetrahedron:
     [[1,2,3,4]]
                                        Type: DeltaComplex(VertexSetAbstract)

EuclideanSpace

home

Where Are You

This is one of a series of pages about topology, these pages start here.

For other pages, on the site, about topology see:

• Open Sets
• Fibre bundles
• Simplectical Complexes
• Delta Complexes
• Homotopy
• Homology

Computer Code Implementation

I have written some code to implement algebraic topology structures. This is described on the page here and the actual code is on GitHub here.

Topological Space and Simplicial Sets (Geometric Realisation)

Topological spaces have some nice properties, they have the concept of nearness in the most general way. However topological spaces have some quite stringent requirements, geometric realisation gives use a way to embed any CW complexes or simplicial set as a topological space.

A first thought for how to embed simplicial sets in topological spaces might be to equate each simplex with an open set, unfortunately this won't work for the following reasons:

• Every union of simplices in a CW complex is not a simplex but unions of open sets must be open sets.
• Every pair of simplices don't necessarily have an intersection.

There is a way to canonically get a topological space from a simplicial complex, this requires a much higher dimensional space so its not very intuitive. For instance, to encode a graph (2D complex), each vertex in the graph needs to have its own dimension in the topological space.

Here we want to encode a complex with two points and a line. We embed this in 2 dimensional Euclidean space (and therefore topological space).

Each of the points is now a vector in its own dimension, these are [1,0] and [0,1] and they are the basis vectors. The line is a straight line between these basis vectors, parameterised by t like this { (1-t)*[1,0]+t*[0,1] | t[0,1] }.

A more complex graph gives a lot more dimensions which makes visualising the topological space harder.

For more information about geometric realisation see the page here.