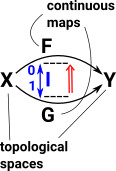On a previous page we defined a homotopy is a continuous map from the product of intervals to the topological space.
[0,1] × [0,1] -> T
with certain properties.
Topological Equivalence
As introduced on page here: In two dimensions it is relatively easy to determine if two spaces are topologically equivalent (homeomorphic). We can check if they:
- are connected in the same way.
- have the same number of holes.
However, when we scale up to higher dimensions this does not work and it can become impossible to determine homeomorphism. There are methods which will, at least, allow us to prove more formally when topological objects are not homeomorphic.
These methods use 'invariants': properties of topological objects which do not change when going through a homeomorphism. Here we look at invariants which arise from homotopy. The page here discusses different invariants which arise from homology, which can be easier to work with but may not be as selective.
Homotopy
 |
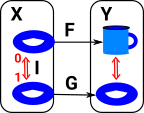
If we have two topological spaces X & Y with two continuous maps between them F & G then a homotopy is a continuous map between F & G. In order to see how this is related to the map between the cup and torus I have drawn a map from a third shape (in this case another torus). So as F continuously maps the G then the cup maps to the torus. |
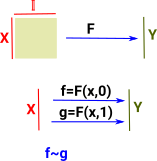
We can move the continuous map forward from the functions to the domain so the functions are homotopic if:
where:
We can think of this as 'filling in' the gap between F and G so that we can take any path through it. |
 |
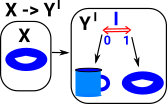 |
Or we can draw it in the codomain (currying) so that each element in X maps to I->Y. |
More about homotopy on page here.
Homotopy Equivalence
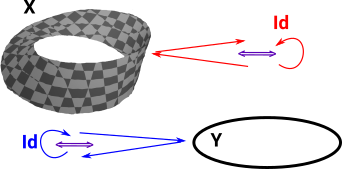
If we continuously map every point in X to a point in Y and require an inverse map which brings the point back to where it started and do this in both directions we get a homeomorphism. But if we want a homotopy equivalence (shapes which can be continuously deformed into each other) then we only need a weaker requirement that this round trip and the identity maps are a homotopy. |
 |
More about homotopy equivalence on the page here.
Homotopy
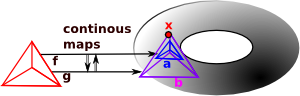
| In homotopy we use equivalence classes between a circle and loops (which don't collapse) on the topological object that we are investigating. We can get further invariants by extending the circle to the surface of higher order n-spheres. | 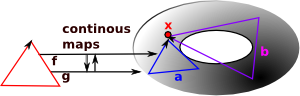
 |
We can then get algebraic structures (mostly groups) by investigating what happens when these loops are composed, the loops are generators of the group. In homotopy the order of these compositions can be significant, that is the groups are not necessarily Abelian.
The fundamental group of a pointed space (mostly represented here by simplicial complexes) is isomorphic to the fundamental group of the space (Seifert-Van Kampen theorem).
The homotopy group is finitely presented by generators and relations. This representation of a group is not, in general, algorithmically computable into other representations of a group.
We can therefore compute 'a' (not 'the') homotopy group for a given simplicial complex. We may also be able to apply some simplifications to this group. However, in the general case, we cannot determine if this is the simplest representation or determine if two such groups are isomorphic (their corresponding simplicial complexes are homeomorphic).
Despite these fundamental limits on what is theoretically possible I still believe it is worthwhile to have the capability to generate 'a' homotopy group for a given structure.
We look at loops of maps from a point to the given space. Each loop, in the space, from the point back to itself is a generator for the group. These loops can then be composed. |
 |
In the following I have drawn circles as triangles because we are representing topologies as simplicial complexes.
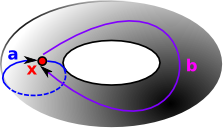
| The simplest homotopy group is the fundamental group. It determines when two paths, starting and ending the point, can be continuously deformed into each other. It records information about the shape in terms of holes in the topological space. |  |
The circle 'a' is homotopic to the circle 'b' if there are continuous maps between f and g. That is 'a' can be continuously deformed into 'b'.
| nth homotopy group. Instead of mapping a circle onto our topological space we map a sphere or higher order n-sphere onto the space. |  |
Calculating Fundamental Group
The simplest homotopy group is the fundamental group. It determines when two paths, starting and ending at a given point (that is loops), can be continuously deformed into each other. It records information about the shape in terms of holes in the topological space.
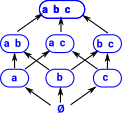
To generate the fundamental group from a simplicial complex:
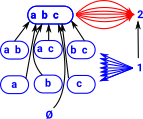
We want to compute edge-path group so we treat the 1-skeleton as a graph. As an example see the graph on the right: |
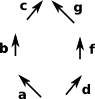 |
Choose a root and generate the spanning tree for the 1-skeleton. In this example, the tree is the blue arrows (a,b,c,d and f). |
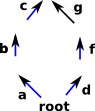 |
| Now we select the edges that are not in the tree, shown in red in the example, these are the groups generators. groups generators: edges in 1-skeleton not in spanning tree |
 |
| groups relations: for every 2-simplex -- e0 e1^-1 e2 -- (e0,e1,e2 are edges) |
Fundamental Groupoid
Finite Group Presentations
Example 1 - A Tetrahedron
I have tried to draw a tetrahedron with its vertices, edges and triangles all indexed:
For more notes about numbering these indexes see page here. |
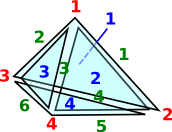 |
The procedure is then as follows:
|
|
|
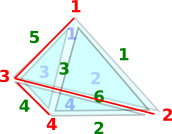 |
|
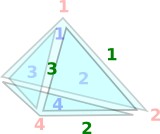 |
|
|
|
|
|
|
Example 2 - Projective Space
Here is an example for projective space:
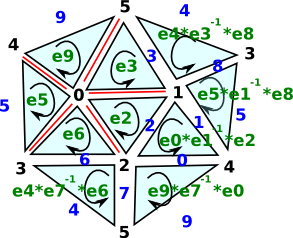 |
keyblack index = nodes |
- Choose the base point as the node labeled '0' in the diagram.
- Calculate a tree where the root is the base point. To do this we remove all edges that would cause a loop. This leaves the edges shown in red as the tree.
- Index all the other links (not in the tree), Shown in blue. These are the generators.
- For each face (2-simplex) we have a rule consisting of the (upto 3) edges=generators taking the inverse of the middle one.
- We now have the generators and rules of the group.
- We can try to simplify if possible and practical.
Indexing Edges
We have to be careful when working out the index numbers for edges. If we get this right the rules can correspond very nicely with the rules for other mathematics such as determinants.
Assume that the nodes are already indexed and that we want to use this to calculate the indexing for the edges. Since the nodes are all indexed, then each triangle will have a node which has the smallest value, a node with with the highest value and an index in between. On the diagram, on the right, I have called these low, medium and high. We can therefore assign a positive direction to each edge so that the arrow goes from a lower to a higher value. |
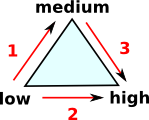 |
We can then number the edges as shown on the diagram.
If we then reverse the direction of the middle arrow (2 in this case) then this will define a winding direction for the triangle.
This alternate inversion of quantities is reminiscent of other mathematical structures.
Examples of Fundamental Group with FriCAS Output
| Space | FriCAS Output |
|---|---|
Disk<e | > - trivial group |
fundamentalGroup(sphereSolid(2)$SimplicialComplexFactory)
(1) < | >
Type: GroupPresentation |
Circlefree group on 1 generator. <a | > |
fundamentalGroup(sphereSurface(2)$SimplicialComplexFactory) (76) <c | > |
Sphere solid<e | > - trivial group |
fundamentalGroup(sphereSolid(3)$SimplicialComplexFactory)
(2) < | >
Type: GroupPresentation |
Sphere surface<e | > |
fundamentalGroup(sphereSurface(3)$SimplicialComplexFactory)
(4) < | >
Type: GroupPresentation
|
Band
|
fundamentalGroup(band()$SimplicialComplexFactory)
(5) <m | >
Type: GroupPresentation |
Möbius Band
|
fundamentalGroup(moebiusBand()$SimplicialComplexFactory)
(6) <k | >
Type: GroupPresentation |
Torus solidZ - Integers - free abelian group |
|
Torus surfaceZ2 <a,b | a b a-1b-1> |
fundamentalGroup(torusSurface()$SimplicialComplexFactory)
- 1 - 1
(7) <o t w | o*w *t o*t*w >
Type: GroupPresentation
We could do additional simplification here |
Union of 2 circlesEquivalent to plane with 2 points removed.
free group on 2 generators. <a,b | > |
|
Union of n circlesfree group on n generators. <a,b,c... | > |
|
Projective space<a | a2> |
fundamentalGroup(projectivePlane()$SimplicialComplexFactory)
(8) <p | p*p>
Type: GroupPresentation |
KleinBottle |
fundamentalGroup(kleinBottle()$SimplicialComplexFactory)
- 1
(9) <v w z | w*z *v v*z*w>
Type: GroupPresentation |