Simplicial complexes allow us to code finitely defined topological spaces in a systematic way.
I have put the code here.
Introduction
A 'simplex' is a set of vertices such that every subset is included in the simplex. For example a tetrahedron contains all its faces, lines and points.
A 'simplicial complex' is a set of these simplexes which may have vertices in common.
Because each simplex contains its subsets, this is a combinatorial structure. When used in this way the structure is known as an 'abstract simplicial complex' optionally we can also associate a point in a space with each vertex, in this case the structure is known as an 'geometric simplicial complex' and it has geometric/topological/homotopy properties.
It is intended that this code is able to be able to support both abstract and geometric simplicial complexes.
Three types of cell complex are implemented:
|
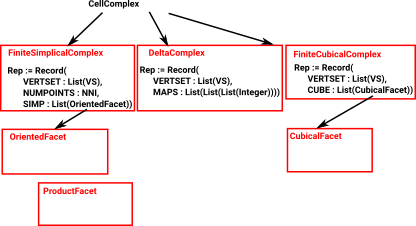 |
Creating Simplicial Complexes
Here are 3 ways to construct a simplicial complex:
Using SimplicialComplexFactory - This allows common complexes to be easily created. Here is an example of building from factory: |
FACTORY:=SimplicialComplexFactory(Integer)
(1) SimplicialComplexFactory(Integer)
Type: Type
(2) -> band()$FACTORY
(2) points 1..6
(1,2,3)
(1,2,6)
(1,5,6)
(2,3,4)
(3,4,5)
(4,5,6)
Type: FiniteSimplicialComplex(Integer) |
Using functions like product, star, link and join to construct complexes from simpler cases. We can join two complexes like this: |
(1) -> ASIMP := FiniteSimplicialComplex(Integer)
(1) FiniteSimplicialComplex(Integer)
Type: Type
(1) -> line := line()$ASIMP
(1) points 1..2
(1,2)
Type: FiniteSimplicialComplex(Integer)
(2) -> simplicialJoin(line,line,true)
(2) points 1..4
(1,2,3,4)
Type: FiniteSimplicialComplex(Integer) |
Build from lists of indexes. Here is an example of building from lists of indexes. This example has 4 points:
|
(3) -> v1:List(List(NNI)):=[[1::NNI,2::NNI],[4::NNI]]
(3) [[1,2],[4]]
Type: List(List(NonNegativeInteger))
(4) -> sc1 := simplicialComplex([],4,v1)$ASIMP
(4) points 1..4
(1,2)
(4)
Type: FiniteSimplicialComplex(Integer) |
Representation of Simplicial Complexes
The FiniteSimplicialComplex representation holds whole Simplicial
Complex. This consists of:
- A vertex set, which can be a list of points, or a list of any
AbelianGroup defined by the type parameter. This allows us to
define a 'geometric simplicial complex' or alternatively to hold
information used for cochain. - A NNI holding the total number of points. This allows us to
reserve unused points. - A list (representing set - no duplication, order unimportant) of
OrientedFacet. Each OrientedFacet defined in terms of points.
If the dimension given for the simplicial complex is 'k' then:
- The number of elements in each vertex = k.
- The maximum number of vertexes in each simplice = k + 1.
For example, a triangle has 3 vertexes, so it is maximum size face in 3-1=2 dimensions.
| dimension | vertex | simplice - (faces) |
|---|---|---|
| 0 | 0 elements | point |
| 1 | 1 element vertex | line - (edge) |
| 2 | 2 element vertex | triangle |
| 3 | 3 element vertex | tetrahedron |
| n | n element vertex | simplice |
So to represent this structure we use the following representation:
Rep := Record(VERTSET : List(VS), SIMP : List(OrientedFacet))
where:
- VS is a vertex in whatever form we are using.
- NNI is an index.
- OrientedFacet represents an individual simplex.
Delta Complex
The above representation defines faces, of any dimension, by their vertices. This is an efficient way to define them, the only disadvantage is that intermediate parts, such as edges, are not indexed. It is sometimes useful to be able to do this, for example, when generating homotopy groups such as the fundamental group.
To do this we represent the complex as a sequence of 'face maps' each one indexed into the next.
As an example consider the representation for a single tetrahedron:
| The usual representation would be: | (1,2,3,4) |
| which is very efficient but it does not allow us to refer to its edges and triangles. | |
Here we have indexed:
|
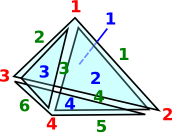 |
| This representation holds all these indexes so that we don't have to keep creating them and they can be used consistently. | |
Face MapsSo the tetrahedron indexes its 4 triangles, each triangle indexes its 3 edges and each edge indexes its 2 vertices. Each face table therefore indexes into the next. To show this I have drawn some of the arrows (I could not draw all the arrows as that would have made the diagram too messy). |
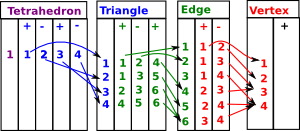 |
Since edges, triangles, tetrahedrons, etc. are oriented we need to put the indexed in a certain order.
| Edges are directed in the order of the vertex indices. That is low numbered index to high numbered index: | 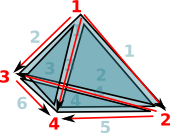 |
For triangles we go in the order of the edges, except the middle edge is reversed. On the diagram the edges are coloured as follows:
This gives the triangles a consistent winding |
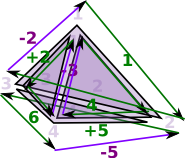 |
| However the whole tetrahedron is not yet consistent because some adjacent edges go in the same direction and some go in opposite directions. | 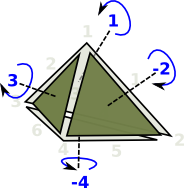 |
| This gives the orientation of the faces as given by the right hand rule. That is: if the thumb of the right hand is outside the tetrahedion, pointing toward the face, then the fingers tend to curl round in the direction of the winding. |
I have put more information about delta complexes on the page here.
Abstract Simplicial Complex vs. Geometric Simplicial Complex
If we apply the restrictions explained so far we have an abstract simplicial complex, However, for a geometric simplicial complex there are some additional conditions.
The additional tests for a geometric simplicial complex are described on the page here.
An Abstract Simplicial Complex is purely combinatorial, that is we don't need the geometric information.
Therefore the AbstractSimplicialComplex domain does not need coordinates for the vertices and they can be denoted by symbols.
Simplicial Maps
Allow edges to be collapsed into vertices.
Oriented Simplexes Maps
Because the code uses Lists instead of Sets the simplexes are oriented by default, if that is not needed then we can just ignore the order.
Topological Aspects of Simplicial Complexes
| We implement topological aspects of simplicial complexes such as boundaries and cycles.
The code for this is explained on the page here. |
 |
Operations on Simplicial Complexes
- Closure - closure of X contains X and all the faces touching X
- Star(A,b) -set of sub-simplices of 'A' which contain face 'b'.
- Link - The 'link' of a simplicial complex and a vertex contains
the boundary of the simplexes of s which include simplex. - Join - We will call it a SimplicialJoin since it is not related to joins in lattices.
- Products are quite complicated so I have put this on a separate page here.
| Here are some examples, first we setup some simplicial complexes to work with: | (1) -> ASIMP := FiniteSimplicialComplex(Integer)
(1) FiniteSimplicialComplex(Integer)
Type: Type
(2) -> v1:List(List(NNI)) := [[1::NNI,2::NNI,3::NNI],[4::NNI,2::NNI,1::NNI]]
(2) [[1,2,3],[4,2,1]]
Type: List(List(NonNegativeInteger))
(3) -> sc1 := simplicialComplex([],v1)$ASIMP
(3) points 1..4
(1,2,3)
-(1,2,4)
Type: FiniteSimplicialComplex(Integer)
(4) -> sort(sc1)
(4) points 1..4
(1,2,3)
-(1,2,4)
Type: FiniteSimplicialComplex(Integer)
(5) -> v2:List(List(NNI)) := [[1::NNI,2::NNI]]
(5) [[1,2]]
Type: List(List(NonNegativeInteger))
(6) -> sc2 := simplicialComplex([],v2)$ASIMP
(6) points 1..2
(1,2)
Type: FiniteSimplicialComplex(Integer) |
| Now we can calculate a boundary. Note that this corresponds to the red line on the diagram above. | (7) -> boundary(sc1)$ASIMP
(7) points 1..4
-(1,3)
(2,3)
(1,4)
-(2,4)
Type: FiniteSimplicialComplex(Integer) |
| Now we can test star, join and link. | (8) -> star(sc1,orientedFacet(1,[4]))
(8) points 1..4
-(1,2,4)
Type: FiniteSimplicialComplex(Integer)
(9) -> link(sc1,orientedFacet(1,[4]))
(9) points 1..4
-(1,2)
(1,4)
-(2,4)
Type: FiniteSimplicialComplex(Integer)
(10) -> cone(sc1,5)
(10) points 1..4
(1,2,3,5)
(1,2,4,5)
Type: FiniteSimplicialComplex(Integer)
(11) -> boundary(sc2)$ASIMP
(11) points 1..2
(1)
-(2)
Type: FiniteSimplicialComplex(Integer)
(12) -> simplicialJoin(sc1,sc2,false)
(12) points 1..6
(1,2,3)
-(1,2,4)
Type: FiniteSimplicialComplex(Integer) |
We can also calculate products and sums of simplicial complexes. Products are quite complicated so I have put this on a separate page here.
Vertex Set Code
We want an indexed set of points, the simplest way to do the indexing is to use 'List' instead of 'Set'.
The vertices themselves may be either:
- literal coordinates.
- symbolic vertex names.
- numeric indexes.
So we cave a category that can represent any of these types and then a domain for each type.
Next Steps
- The additional tests for a geometric simplicial complex are described on the page here.
- The way we implement topological aspects of simplicial complexes such as boundaries and cycles is explained on the page here.
- To generate the fundamental group from the simplicial complex see the page here.
- Products are quite complicated so I have put this on a separate page here.
Bibliography
For more details see:
- [1] Mathematics++ Kantor,Matousek,Samal 2015 ISBN 978-1-4704-2261-5 Chapter 6 - Topology. Contains a relatively gentle introduction to homology.
- [2] Graphs, Surfaces and Homology, Peter Giblin 2010 ISBN 987-0-521-15405-5
Builds up to homology groups via graphs and simplicial complexes. - [3] Wikipedia
- [4] this page
- [5] Finite simplicial complexes in Sage
- [6] Finite simplicial complexes in NPM
- [7] Simpcomp - a GAP package for working with simplicial complexes
- [8] A Macaulay2 package for working with simplicial complexes
- [9] Hatcher - Algebraic Topology - book also available free online.
- [10] Computational Geometry - Algorithms and Applications by Mark de Berg, Otfried Cheong, Marc van Kreveld and Mark Overmars
This book looks at the algorithms from a computer science, rather than pure mathematics, point-of-view. So homotopy or homology is not mentioned but subjects like Voronoi Diagrams, Delauney Triangulations, Convex Hulls and many similar topics are covered.