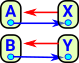
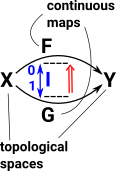Here we discuss continuous mappings between topological spaces.
| For example, the continuous 'rubber geometry' deformations as between a toroid and a mug. |  |
Continuous Maps
A function is continuous if it doesn't jump, that is, when two inputs of the function get close to each other then the corresponding outputs of the function get close to each other.
Here we discuss the most general form of continuous map which also applies to non-metric topological spaces.
A continuous mapping implies a limited kind of reversibility, at least locally.
Definition 1
Here is one definition of continuity, based on open sets:
| Let X and Y be topological spaces. A function f : X->Y is continuous if f-1(V) is open for every open set V in Y. |  |
Definition 2
Another definition of continuity, based on neighbourhoods, is equivalent to the above definition.
Let X and Y be topological spaces. A function f : X->Y is continuous if for every x X and every open set U containing f(x), there exists a neighbourhood V of x such that f(V) U. |
 |
More detail about continuity on page here.
Continuous Surjective Maps
 |
Here is an extreme case of a Surjective Map which maps to a single point. This seems to meet the requirements as there is an open set round the whole preimage. We can think of surjections which meet these requirements as 'nice surjections'. See fibrations |
Continuous Injective Maps
 |
Here is an extreme case of a Injective Map which maps from a single point. In this case all the open sets in the codomain need to map back to a single open set in the domain. This meets the requirements so it is a 'nice injection'. See cofibrations |
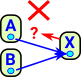
Map from Interval
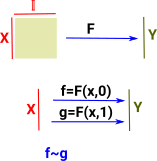
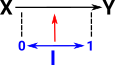
Start by thinking of the interval as a continuous line segment from 0 to 1. So a map from I represents all possible values between X and Y. A homotopy is a higher level map between two maps. |
 |
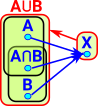
Homotopy
 |
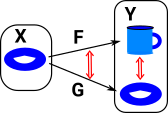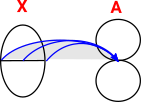
If we have two topological spaces X & Y with two continuous maps between them F & G then a homotopy is a continuous map between F & G. In order to see how this is related to the map between the cup and torus I have drawn a map from a third shape (in this case another torus). So as F continuously maps the G then the cup maps to the torus. |
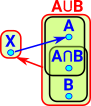
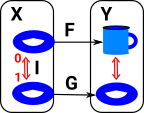
We can move the continuous map forward from the functions to the domain so the functions are homotopic if:
where:
We can think of this as 'filling in' the gap between F and G so that we can take any path through it. |
 |
H: X × [0,1] -> Y |
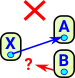
Or we can draw it in the codomain (currying) so that each element in X maps to I->Y. |
More about homotopy on page here.
 |
Maps F & G are homotopic if:
where:
We can think of this as 'filling in' the gap between F and G so that we can take any path through it. There is a good video about this on a site here. |
A homotopy is a function between functions with certain properties.
Let X and Y be topological spaces and f,g : X->Y be two continuous maps. Then f is said to be homotopic to g (written f~g) if there exists a map F : X× where:
|
 |
-> Y, called a homotopy such that F(x,0) = f(x) and F(x,1) = g(x) .Homotopy Equivalence
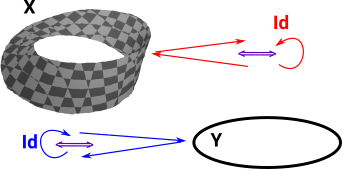
If we continuously map every point in X to a point in Y and require an inverse map which brings the point back to where it started and do this in both directions we get a homeomorphism. But if we want a homotopy equivalence (shapes which can be continuously deformed into each other) then we only need a weaker requirement that this round trip and the identity maps are a homotopy. |
 |
More about homotopy equivalence on the page here.
There is a good video about this on a site here.
Fibrations and Continuous Maps
Some continuous maps between spaces have a 1:1 mapping between points, these continuous maps are known as homeomorphisms. It is also possible to have a continuous map from a line to a point, or vise versa, that is what we are discussing here.
 |
There is a continuous map from a line to a point. In the same way that in sets, attempting to reverse a surjective map leads to fibre bundles, with continous maps we get fibrations. |
 |
This continuous map is reversible so we have a continuous map from a point to a line. |
| So, for example, two circles that touch at a point can be continuously deformed into a circle with a line through the middle. |  |
Or we can expand all the points on, say a circle, to get a band. This is like a product of a circle and a line. |
 |
For more information see:
Fibrations and Cofibrations
A continuous map (homotopy equivalence) can be decomposed into 3 types of continuous map: weak equivalences, fibrations and cofibrations. This is very similar to the way sets can be decomposed into bijections, surjections and inclusions.
Comparison of Model Category and Set Category
Model categories are introduced on page here.
| Set Category | Model Category | |
|---|---|---|
ObjectsIn category theory set objects are often thought of as 'n' elements without any further structure (just an unconnected set of points) or empty set. In model theory objects are spaces, say a topological space with a subobject structure. |
 |
 |
MorphismsIn both cases mappings can be decomposed into 3 types:
|
|
|
reversing this leads to fibre bundles |
||
reversing this leads to equivilance classes and logic. |
For more comparison of model category and set category see page here.
What does a continuous mapping look like?
| A continuous mapping may collapse multiple points to single points. |  |
| Here we convert that to neigbourhoods. |  |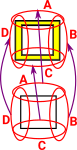
 |
So this looks like a fibre bundle as discussed on the page here.
Counter Examples
 |
|
 |
Examples - Möbius Band to Circle
| Here we have a morphism which collapses the width of the Möbius band. |  |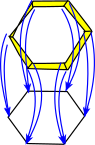
| when we reverse this morphism we keep the global structure and loose some local structure. We also loose the twist in the Möbius band. |  |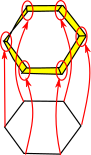
Examples - Helix to Circle
| Here we have a morphism which collapses a helix to a circle. |  |
 |
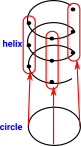Homeomorphisms
A homeomorphism preserves 'nearness' but allows 'rubber geometry' deformations. Note: homeomorphism is a different concept from homomorphism. |
 |
Projections
| We can project helix onto circle and still keep continuity. |  |
Homotopy Extension Property (HEP)
| Lets consider mapping f0 from a topological space X to a topological space Y. How can we determine if this mapping is a continuous mapping? We have already seen a possible answer to this above (f0 : X->Y is continuous if f0-1(V) is open for every open set V in Y). There are other ways to determine this if we don't have details of open sets. |  |
 |
Here is a example, its obvious just by looking at it that this map is continuous, we can just deform X to get Y (its got the same number of holes) but some maps may not be continuous and it may not be obvious. So we need to formalise it. |
| Sometimes we have an additional piece of information. That is that there is a subset of X called A, this has a map into Y that is known to be continuous, this is f0 restricted to A denoted: f0|A . So the question is: when can this continuous map be extended to the whole of f0 ? |  |
 |
To be sure to map to Y can be extended the map from X to its subset A must be a retraction. A retraction is a surjective map that is continuous. This ensures that A has the same number of holes as X. |
This diagram is intended to show the homotopy and the mappings along the interval. To do this the topologies X, A and Y are shown as some sort of one dimensional projection. So the whole mapping is shown as X×I starting at X×{0} and mapping to Y at X×{1}. |
 |
 |
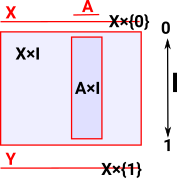This is often illustrated in terms of category theory diagrams (for instance wiki here). This diagram is rotated compared to the diagrams above. Here the map from the interval is curried. So YI is all the maps out of the interval I->Y. Instead of having X×I -> Y we have |
There is a good video about this on a site here.
Homotopy Extension Property (HEP) - Example
Here is an example of a Cofibration showing the homotopy extension property (HEP)
 |
Here we have three topological shapes:
|
A is a subspace of X so the map from A to X is an injective mapping. The pair [X,A] has the HEP if certain conditions are met.
The arrow from A to Y is a homotopy h: A×[0,1] -> Y (it is a continuous family of maps from a point to a line).
 |
We also have a map F:X->Y. Because this is a single map we cant map the point to the line (bar in Θ). |
We need to be able to extend the map F:X->Y to the homotopy H: X ×[0,1] -> Y. This is what the HEP allows us to do. |
 |
As Continuous Map
 |
Here we are looking for a continuous map to map a topological space to map to something homotopy equivalent. As explained on page here a function f : X->Y is continuous if f-1(V) is open for every open set V in Y. Can we treat simplcies like open sets? So the simplcies map in the opposite direction to vertices? The simplcies may map to simplcies of a different dimension, so here the middle bar (edge) maps to a vertex. This continuous map should preserve loops, does this do that? can we prove it? |
More information:
HEP and Topos Theory
Relationship to topos theory.
| If we look again at the category theory diagram for the HEP. | |
and then compare it to the diagram for the sub-object classifier (see page here) we can see that there is a similar thing going on: In the Topos case there may not be a requirement for continuous mappings but S is a subobject of X and the mapping between them is injective. |
 |
HEP and Kan Extensions
Relationship to Kan extensions.
| Starting again at the category theory diagram for the HEP. | |
| Compare it with the diagram for the Kan extension (see page here). The HEP appears to be a special case of the Kan extension (most things are!) so, in this diagram, 'F' is a constant mapping and 'K' is injective. |  |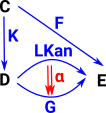
| In order to make F constant we factor it through the terminal object. |  |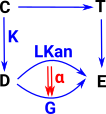
Next
see pages about:
