There are various categories associated with topology. The most fundamental is:
Top - The Category of Topological Spaces.
 |
It has:
In the most general definition the points map like sets and there is an additional requirement that the pre-image of an open set is an open set. That is the open sets map in the reverse direction. The isomorphisms in this category correspond to homeomorphisms in topology. |
 |
This is a category because the composition of two continuous maps is also a continuous map. The composition is f•g for points and
note: change of order for open sets. |
| Also the Id is the Id for points and the Id for open sets. |  |
Top has some nice properties, it preserves limits and co-limits, but it does not have exponential objects for all spaces and so it does not have some properties we would like: it is not cartesian closed or a topos.
See page here about categorical limits.
If these properties are required then there may be variations of Top for the spaces required that have these properties. For example, nice topological spaces such as compactly generated topological spaces.
Other Categories that may have better properties Simplicial sets are co-limits of Top. |
|
Weak Equivalences
Since injection and surjection are not homotopy invariant notions (consider an interval embedding into the real numbers vs. an interval mapping to a point), we do not have the notion of a functor being "full" or "faithful." However, we can define a functor of quasi-categories to be fully faithful if for every X and Y in C, the map FX,Y is a weak equivalence. (from Wiki page).
Full & Faithful Functors
|
C and D are locally small categories.
see wiki page |
See page here for more about weak equivalences.
Homotopy Category
- The objects topological spaces
- The morphisms are homotopy classes of continuous maps.
Or start with a model category and define its associated homotopy category, with a construction introduced by Quillen.
see homotopy category at ncatlib.
Other Categories
There is a category of the subset structure of open sets. There are also categories of fibres and sheaves.
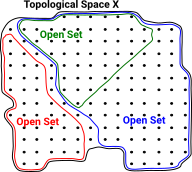
Subset Structure of Open Sets as Category
Subsets give interesting structure to open sets. This allows us to define a category of topological spaces. We can also further elaborate this subset structure to get fibre bundles and sheaves.
In this diagram the open set U is a subset of V. U We can represent this as an arrow from V to U V->U |
 |
This has the properties we expect from a category, for instance, the identity map: U->U (identity map) |
 |
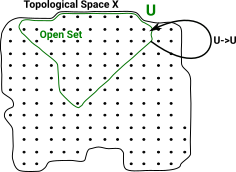and composition (U->V)*(V ->W) = U->W (composition) |
 |
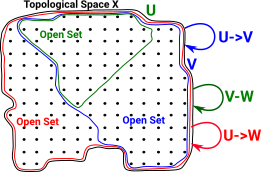VFor a non-category theory view of this structure see page here.
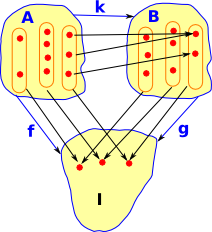
Bn - Category of Bundles
A fibre bundle is a function f:(A->I) This is described on the following pages: |
 |
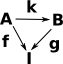We can make this a category where:
This triangle must commute. So the elements (germs) of a stalk in 'A' must map to the same stalk in 'B'. This is a comma category as discussed on this page. |
 |
The Bn Category can lead on to the concept of a Topos.
For more information about the Bn category see this page.
Simplical Sets
We have looked at these, mostly from a topology point of view, on the pages here:
The subject can also be approached from a purely combinatorial point of view.
Here we investigate how these structures can be viewed in a category theory way.
Δ is a category with:
The morphisms are inclusions |
 |
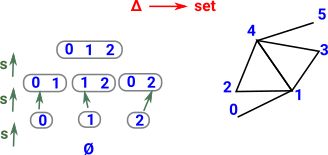| Δop is a category with the same objects but morphisms are the face maps. |  |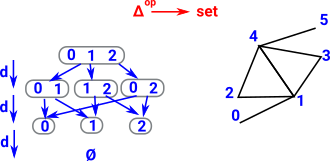
Category of Presheaves
Objects: Cop -> setcontraveriant functors X: C -> set (written X: Cop -> set to indicate contraveriance) |
 |
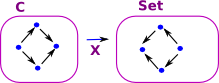Morphisms:are natural transformations N: X -> Y |
 |
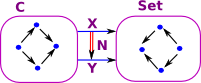For a non-category theory view of this structure see page here.