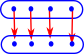
On these pages we look at both equality between terms and equality between types (and how they are related).
Equality of Sets
To get some intuition lets first look at equality between sets. There are multiple ways to define 'equality' between sets. Here I have divided them into 'internal' or 'external' depending whether they look inside the set.
| 'Internal Equalities' | 'External Equalities' |
|---|---|
Explained below |
Explained below |
 |
The traditional way to define equality of sets, in set theory, is to say two sets are equal if they contain the same elements.
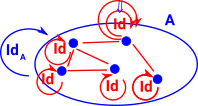
Equality of Types in MathematicsIn mathematics the natural way to relate types is often to use a weaker form of equality called isomorphism. IdA = G•F However, for checking the type consistency above, this is too loose. For example, the types A×B and B×A are isomorphic and they might hold the tuples (a,b) and (b,a) which are not the same without swapping the first and second elements. |
Note: that this definition of isomorphism requires another type of 'equality' called Id. So, in the end, the definition of 'external' equality still requires an 'internal' equality but a very simple one.
Extensionality
In logic, extensionality, or extensional equality, refers to principles that judge objects to be equal if they have the same external properties.
Equality of Terms
If we have a simple type, such as Nat, it should be fairly simple to determine equality between numbers. For example the compiler can tell that 1=1 and 1≠2.
However, for these purposes, we are usually working with terms (expressions). So, instead of comparing elements of Nat it is like comparing elements of Expr Nat. This means we have to determine potential equalities like: 2*3=5+1.
To do this both sides of the equation are normalised (evaluated) to give us 6=6 in this example and then the equality is checked.
However these expressions can also contain variables and this is where things start to get more complicated. It is still possible that the compiler can do a certain amount of normalisation but exactly what will normalise will depend on the compiler and there are usually equalities that are true but don't normalise to a definitional equality.
It is not always obvious which expressions will normalise further and which won't. For instance x+0 may normalise to x but 0+x may not normalise any further.
Equality of Functions
Two functions are equal if their values are equal at every argument.This is known as functional extensionality.
Equality of Types
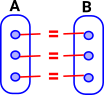
We can move from talking about equality of sets to equality of types. Instead of the concept that two sets are equal if they have the same elements we may be able to use the idea that two types are equal if they have the same constructors.
| 'Internal Equalities' | 'External Equalities' |
|---|---|
Explained below |
Explained below |
Equality of Properties
Equality is a property, but what about equalities between properties? That is equalities between equalities (higher order equalities). How do we determine these?
in simple cases an equality could be represented by a Boolean value, in which case properties would be equal if they were both true or both false, however here we are using inhabited types to indicate truth and uninhabited types represent unproven. So how do we represent equality between these?
A naive approach might be to define equality of properties like this:
| proven | proven | equal |
| proven | unproven | unequal |
| unproven | proven | unequal |
| unproven | unproven | equal |
but that's not really in the spirit of M-L type theory, how do you test if something is unproven?
Here is a proof of Leibniz equality. (using Arend Theorem Prover) In Arend idp is just reflexitivity (Refl) idp : a = a |
\func Leibniz {A : \Type} {a a' : A}
(f : \Pi (P : A -> \Type) ->
\Sigma (P a -> P a') (P a' -> P a)) : a = a'
=> (f (\lam x => a = x)).1 idp |
An approach is to say the property of a is equal to the property of a' if P a implies P a' and P a' implies P a.
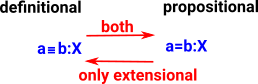
Definitional and Propositional Equality
Here we are looking at the relationship between two types of equality: definitional equality and propositional equality.
In Nat consider 'n', '0+n' and 'n+0' they are equal terms in some way. In Idris 'n' and '0+n' are definitionally equal because they automatically normalise to the same. Definitionally equality is sometimes denoted with a 3-bar equals sign (≡) or just by using the same symbol. But 'n+0' is propositionally (but not definitionally) equal to n. It is denoted with a normal equals sign (=) and shown as an arrow between nodes. |
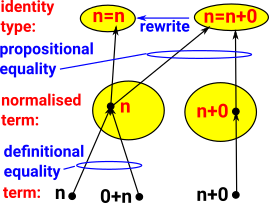 |
- Definitional equality is sometimes known as judgemental equality.
- Propositional equality is indicated by the presence of an inhabited identity type (id).
Equality of Types and Terms
Because we are working in dependant type theory we need to be able to determine the equality of:
- terms
- types
- type families (types that depend on terms)
- and so on for higher orders,
This leads to a complex structure, for these equalities, which can be represented by a setoid (see page here) or groupoid (see page here).
One of the main differences between set theory and type theory is that terms (elements in set theory terminology) only exist within the type they are defined in.
So, if we have an term x:A and we need to express it like this x:B we need to know that A and B are effectively the same type, close enough that it makes no difference. This is an identity (Id).
Equality of Types
A and B can only contain the same term if they are the same type: equality conversion rule |
For discrete types, it is easy to know if they are identical, for instance:
- Integer is not identical to Boolean.
- Integer is identical to Integer.
The interesting cases are for dependent types. How do we determine if members of a type family are identical? Here C(A) is a type family that depends on A: |
||
If x and y are propositionally equal then C(x) is identical enough to C(y) to be treated as the same type. [ref Homotopy Type theory: Univalent Foundations - Section 1.12 Identity Types] |
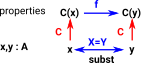 |
| So if we have a type family C and a function f like this: | C : T -> Type f : x:T -> y:T -> (x=y) -> C(x) -> C(y) |
|
| Then C(x) will be identical to C(y) and can be exchanged and treated the same in a program. | f(x,x,refl) = Id |
At first it looks like the function f is partial in that, we could put any values for x and y, but it is only valid when x=y. However, for programs like Idris, x=y will be checked at compile time and so cannot be run unless x=y (a proof exists that x=y).
Type Checking in Computer Programs
At compile time the compiler will need to check that types are consistent and what is expected.
In the case of dependent types equality of types will depend on equality of terms. For example, if we are adding two vectors we require the lengths to be the same, so we need to be able to prove the equality of the lengths even if they are variables.
Theories
| There are different type theories, with different uses, depending on the way properties are preserved under different definitions of equalities. | 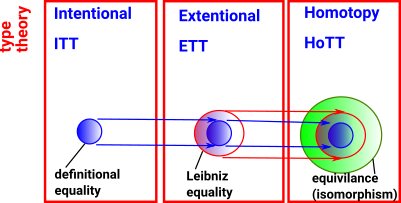 |
ETT Extensional Type Theory |
ITT Intentional Type Theory |
HoTT Homotopy Type Theory |
|
|---|---|---|---|
| Equality Used | Exact equality (after normalisation) | Leibniz equality | Equivalence |
| see page here | see page here | see page here |
In M-L extensional type theory two types are the same only if they are defined in exactly the same way. This becomes very important for dependent types, for example, vectors can only be added if they have the same length, however (Vect n) and (Vect (n+0)) would be treated as different types in extensional type theory. This means that extensional type theory limits the calculations and checks that can be done.
In M-L intentional type theory two types are the same if they are defined in the same way or if there is a proof that they are equal. However, in intentional type theory, proofs are not canonical for instance to construct a proof we may have to make expressions more complicated before we can simplify them. So there is not a general algorithm for constructing proofs and each proof required may have to be supplied by a human coder.
In homotopy type theory proofs are canonical (canonicity) and therfore automatic but to get this benefit other things get more complicated (conservation of complexity?). In homotopy type theory structures are built constructively rather than having constraints in the form of equations instead we have rules. The intuition for this type theory comes from homotopy.
Definitional Equality
may also be known as:
- Judgemental equality
- External equality
See this page for more information.
Propositional Equality
Propositional equality may also be known as:
- Equality type
- Identity type
- Internal equality
- Liebniz equality (well Liebniz equality is defined differently but we can convert between propositional equality and Liebniz equality so in this context they amount to the same thing, more information about this on this page)
See this page for more information.
There is another type of equality which here is denoted by the usual two-bar equals sign '='.
A=B is a proposition which may, or may not, be true. To prove it is true we need to construct an instance of it. The constructor for such a proof is called 'refl'.
This quality of being equal to itself is called reflexitivity (refl). See equivalence.
Definitional equality can be embedded into propositional equality because if A![]() B then A=B can be constructed.
B then A=B can be constructed.
| Embed definitional equality into propositional equality. |
More about propositional equality and definitionaly equality (with Idris examples) on page here.
Identity (Propositional Equality) Constructor
If we have an identity type |
x = x : Type |
|
then we can construct it with a simple constructor with no parameters |
Refl : x = x |
That is, if x=x is inhabited by Refl that constitutes a proof that x=x.
However this hides a lot of complexity, if we use the same symbol on both sides of the equation - what does that mean? We might say that the meaning comes from the deconstuctor but how is this all implemented?
| In some ways we could think of rewrite as like a second constructor for an equality type. So it behaves a bit like an inductivly defined type where Refl can construct a definitional equality on its own but requires the help of rewrites to | 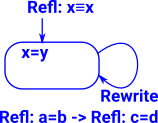 |
Identity (Propositional Equality) Deconstructor/Eliminator
There are also two possible deconstructors/eliminators known as J and K. (K does not apply to some flavors of type theory) In the same way that, in Leibniz equality, equal terms have equal properties we can now consider properties of equalities. |
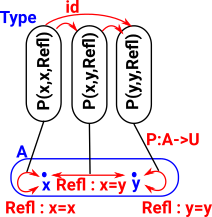 |
The first part 'P' is a dependent type. We could think of it as property which is true for every pair of terms which are equal: (P : (a,b:t) -> (a=b) -> Type) The next part shows that an element of each of these types (Refl) can be constructed and are therefore 'true': ((a:t) -> P a a Refl) The result say that every property that is true for identical things also is true of a thing with itself. ((a,b:t) -> (p:a=b) -> P a b p) |
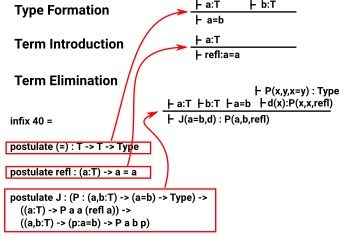
J : (P : (a,b:t) -> (a=b) -> Type) ->
((a:t) -> P a a Refl) ->
((a,b:t) -> (p:a=b) -> P a b p)
J P h a a Refl = h a |
When all properties of a type are the same this is also known as Leibniz equality (see page here) however P is a property of two equal terms.
Axiom J allows the possibility of many equality constructors Refl (although the single name and the pattern matching rules in Idris would prevent that).
Examples Rational NumbersWiki Each number has numerator p and a non-zero denominator q. So P could be defined like this: P : (a,b:t) -> (a=b) -> Type P a b Refl = (ap*bq = aq*bp) So ((a:t) -> P a a Refl) |
If we want to specifically prevent the possibility of multiple Refl constructors then axiom K applies:
Axiom KK : (P : (a:t) -> (a=a) -> Type) ((a:t) -> P a Refl) ((a:t) -> (p:a=a) -> P a p) |
K : (P : (a:t) -> (a=a) -> Type) ->
((a:t) -> P a Refl) ->
((a:t) -> (p:a=a) -> P a p)
K P h a Refl = h a |
K: ΠA:TypeΠx:AΠP: x=x -> Type(P (Refl) -> Πh:x=xP(h))
Asserts that each term of each identity type x=x (of equivalences of a term x:A) is propositionally equal to the canonical reflexivity equality proof Refl:x=x.
Unary predicate by diagonalization of binary predicate J
Cantor's diagonal argument
Another consequence of this is the higher order identity types:
| x=p=qy | [or in the other notation: IdIdA(p,q)(x,y)] |
are always inhabited. This is known as 'uniqueness of identity proofs (UIP).
Extensional and Intentional Type Theory
This is where extensional and intentional type theory start to diverge.
 |
- Extensional equality (ETT) equates things if they are constructed in the same way - If they normalise to the same value.
- Intentional equality (ITT) equates things that behave the same - If every property of x is equal to the property of y (satisfy the same predicates) then x=y.
Extensional type theory has some nice properties when using for computing but undecidable type checking.
Intentional type theory allows programs that may be non-terminating.
Extensional Type Theory (ETT)
Allows provable equations to impact directly on type checking without the need for explicit substitutions.
| If x and y are definitionally equal then they are propositionaly equal. |
|
|||
equality reflection ruleIn ETT only, if x and y are propositionaly equal then they are definitionally equal. That is, the two types of equality are interchangeable. |
|
Undecidable type checking
Program always has normal form
ncatlab - Extensional type theory denotes the flavor of type theory in which identity types must be propositions (of h-level 1). In other words, they are determined by their extensions — the collection of pairs of points which are equal.
Intentional Type Theory (ITT)
Keeps definitional equality and propositional equality more separate.
| As with ETT, If x and y are definitionally equal then they are propositionaly equal. |
|
|||
But the inverse is not true, if x and y are propositionaly equal then they are not necessarily definitionally equal. However, we may be able to turn propositional equality into definitional equality by using a sequence of rewrite/substitution/induction rules. However there is not a general algorithmic way to do this. |
where:
|
So we may need to provide these proofs by adding code to the program.
This allows definitional equality to remain decidable.
But this reduces the power of the propositional equality.
Requires an explicit operation, transporting values between types which are merely provably, but perhaps not definitionally, equal.
Leibniz Equality and Indiscerniblity of Identicals
More about Leibniz equality on page here.
Leibniz equality says that if two terms have the same properties, for all properties, then they are equal. When programming we might represent properties as a function from a term to a type.
|
|
| So if we have a property: | Prop : A -> Type |
| and if we have a proof that x=y where x and y are both of type A: | Refl : x=y |
| and we have a proof that Prop x is true: | Refl: Prop x |
| then Prop y is true: | Refl: Prop y |
| For example, in Idris, replace or rewrite (which has a nicer syntax) |
|
Rewrites
| In order to construct an identity type, such as n=n+0, we need proof that n does equal n+0. In a programming environment we do that by rewriting n=n+0 to n=n and then constructing using Refl. |  |
Rewrite in Idris
See Idris documentation.
prop: Nat -> Type prop x = (x=2) equ: x=y rewrite equ in prop |
This does the following:
|
| Here is a proof in Idris for n=n+0 using the 'rewrite' keyword. | plusReducesR : n = plus n 0
plusReducesR {n = Z} = Refl
plusReducesR {n = (S k)} = let rec = plus_commutes_Z {n=k} in
rewrite rec in Refl |
There is more information about how to write proofs in Idris on the page here.
Rewrite in AGDA
See AGDA documentation.
In AGDA we seem to be able to put the rewrite on the LHS of a function definition where the 'rewrite' keyword translates to a 'with' construction.
plusC : (a b : Nat) -> P (a + b) -> P (b + a) plusC a b t with a + b | plus-commute a b plusC a b t | .(b + a) | refl = t |
This proves that some property of a+b is also true of b+a. |
Formation, Introduction and Elimination of Identity Type Families
Identity Type Families model propositional equality.
Formation: A type exists for every pair of terms in base type
Introduction: The above types are only inhabited if the terms are propositionally equal.
refl: introduces terms. J: eliminates terms. see these sites: |
 |
The elimination rule 'J' for propositional equality can be explaind by thinking of the propositional equality as Leibniz equality as discussed on the page here.
Equality Type Constructor
The equality type only has one constructor which is Refl (short for reflexive).
If we have an equation, such as 1+1=2, this can be constructed using Refl only if the left and right of the equation is the same. We think of this constructor as proof of that the equation is true.
If we have an identity with a variable, such as (x:Nat) -> x = x + 0, then we need to be able to generate a Refl for every value of x. For information about how to do this see the page here.
Equality Type eliminator
This goes in the opposite direction, that is, start with an equality type and take it apart somehow. The equality type eliminator, traditionally called J has two parameters:
A function P which generates a type family. This gives a type for every pair of elements. |
(P : (a,b:t) -> (a≡b) -> Type) |
| A proof of equality for equal elements. | ((a:t) -> P a a Refl) |
From these parameters we can then generate the following function:
((a,b:t) -> (p:a≡b) -> P a b p)
Elimination Rule (J)
Here is the constructor and eliminator for
| Constructor | Eliminator |
|---|---|
Refl |
 |
Where:
- P is a property given by a family of types (type universe) for every pair of terms that are equal. We need to choose a suitable property depending on what we need to prove about identity types.
Why is the elimination rule so complicated for identity types?
Simpler Case of Eliminator for a GroupSometimes it helps to look at a simpler structure first to get some intuition. In the case of a finite group the constructors are the permutations representing the generators. By combining these generators we get other permutations. So the constructor is a set of permutations however, the same group may be generated by different sets of permutations. So what would be the eliminator? The eliminator should not have to choose and one set of permutations when other sets would be just as good. |
In the case of a groupoid the elimination rule (J) determines the induction/recursion principles. J says:
Given:
- A function P which forms a type which depends on two terms of T and a constructor for the proposition a=b.
- A function from a term 'a' to an element of P (gives each terms equality to itself)
we get:
- An term of P for every pair of terms.
Path Induction
The idea of path induction is to prove that a property holds for all identifications between terms in some A it suffices to show that the property holds for all trivial self-identities refl.
Propositional Equality - Identity Type
Identity Type |
|||
|---|---|---|---|
formation rule Id exists for every pair of terms in A |
|
||
term introduction rule reflexitvity Id is only inhabited if both elements of the |
|
||
| term eliminator | |||
| computation rule | |||
Local completeness rule |
Implemetations of Identity Type
Idrisfrom : Idris-dev/libs/prelude/Prelude/Basics.idr |
||| Identity function. id : a -> a id x = x |
|
from : coq/theories/Init/Datatypes.v |
(** [identity A a] is the family of
datatypes on [A] whose sole non-empty
member is the singleton datatype [identity A a a] whose
sole inhabitant is denoted [identity_refl A a] *)
#[universes(template)]
Inductive identity (A:Type) (a:A) : A -> Type :=
identity_refl : identity a a.
Hint Resolve identity_refl: core.
Arguments identity_ind [A] a P f y i.
Arguments identity_rec [A] a P f y i.
Arguments identity_rect [A] a P f y i.
Register identity as core.identity.type.
Register identity_refl as core.identity.refl.
Register identity_ind as core.identity.ind.
(** Identity type *)
Definition ID := forall A:Type, A -> A.
Definition id : ID := fun A x => x.
Definition IDProp := forall A:Prop, A -> A.
Definition idProp : IDProp := fun A x => x. |
Definitional Equality vs. Propositional Equality
Type theory without dependant types is computable in that we can easily type check code. Dependent types allow much more powerful compile-time checking but now we cant be certain that we can type check at compile-time. To understand this dilemma we need to spilt type equality into definitional and propositional equality.
ref: http://www.cs.nott.ac.uk/~psznk/docs/karlsruhe.pdf
Definitional Equality (Judgements) |
Propositional Equality | |||||||
|---|---|---|---|---|---|---|---|---|
| decidable equality | equality needing a proof | |||||||
| for program: | static (syntax) This is the equality the type checker uses, it is equality that can be decided statically, at compile time. |
dynamic (semantics) we may need to run program to determine equality at runtime. |
||||||
| for Curry-Howard | true if ID type can be inhabited (constructed). There is an Id type for every two elements
|
|||||||
| examples |
eta equality is included in some proof checkers Agda and Epigram but not Coq. |
What you use when stating a proposition |
||||||
In set theory (and in logic based on set theory) many propositions are about whether something is an element of a given set (a![]() A). In type theory a term does not exist outside the type therefore, whether a term is part of a type (a:A), is definitional not propositional.
A). In type theory a term does not exist outside the type therefore, whether a term is part of a type (a:A), is definitional not propositional.
| Set Theory | Type Theory | |
|---|---|---|
| Definitional Equality | a membership of a set may be either defined or be a proposition |
a:A |
| Propositional Equality | Id |
Propositional Equality
| For every pair of terms there is an identity type. If these two terms are equal the type can be constructed by Rafl | 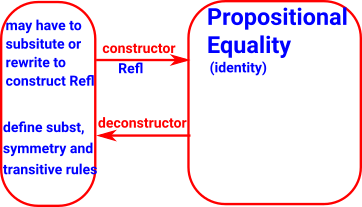 |
The equalities that are supported, or otherwise, by an evidence (a composition of rewrites). - Queiroz, Oliveira.
SetThe first way to construct terms of IdA(x,y) is to use refl. refl : Π(a:A), Id(a,a) This gives a set without additional structure (discrete homotopy). There is a type for every pair of points but only loops are ocupied. |
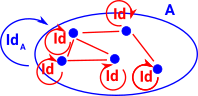 |
1-groupoidsIn addition to refl, for any given type family A(x,y,p) indexed by terms x,y:X and p:Id(x,y) and any given function f : Π(x:X), A(x,x,refl(x)), we have a function J(A,f) : Π(x,y:X), Π(p:Id(x,y)), A(x,y,p) with J(A,f)(x,x,refl(x)) stipulated to be f(x). |
 |
2-groupoids
|
sequent calculus notation:
- Γ
 - Γ is context.
- Γ is context. - Type - is a universe of types (which may be an term in a higher order tower of universes).
- A:Type - A is a type in the universe of types
- A(x):Type - a family of types indexed by term x.
- IdA(x,y):Type - Martin-Löf's identity type - collects the ways that x,y are identified.
- p:IdA(x,y) - terms of Id give a reason why x and y are the same.
- refl:IdA(x,x) - reflexivity proof, every term is equal to itself .
Propositional Equality in Computer Languages
Propositional equality is used in proof assistants but a general language - Idris allows propositional equalities to be declared (see here), allowing theorems about programs to be stated and proved. Equality is built in, but conceptually has the following definition:
data (=) : a -> b -> Type where
Refl : x = x
Equalities can be proposed between any values of any types, but the only way to construct a proof of equality is if values actually are equal. For example:
fiveIsFive : 5 = 5 fiveIsFive = Refl
twoPlusTwo : 2 + 2 = 4 twoPlusTwo = Refl
Id - Identity type
see site here for a good overview
We can interpret equalities between 2 terms 'a' and 'b' as being a computational path between the two terms, that is sequences of rewrites and substitutions that turn 'a' into 'b'.
The collection of all these terms is the identity type Id(a,b).
Ways to constuct terms of IdA(x,y)
refl : Π(x:X), Id(x,x),
In addition to refl, for any given type family A(x,y,p) indexed by terms x,y:X and p:Id(x,y) and any given function
f : Π(x:X), A(x,x,refl(x)),
we have a function
J(A,f) : Π(x,y:X), Π(p:Id(x,y)), A(x,y,p)
with J(A,f)(x,x,refl(x)) stipulated to be f(x).
Then, in summary, the identity type is given by the data Id,refl,J. With this, the exact nature of the type Id(x,y) is fairly under-specified. It is consistent that it is always a subsingleton in the sense that K(X) holds, where
K(X) := Π(x,y:X), Π(p,q:Id(x,y)), Id(p,q).
Using Introduction and Elimination Rules (see ncatlab)
| type formation | For every pair of terms of A we introduce a type IdA which is inhabited when the terms are equal. |
from ncatlab (hypothetical form):
from Warren:
|
||||||||
term introduction reflexivity |
Without univalence, refl is the only given way to construct terms of the identity type. the univalence axiom provides a means of constructing terms other than refl(x), at least for some types, and hence the univalence axiom implies that some types are not sets. (Then they will instead be 1-groupoids, or 2-groupoids, ∞-groupoids. |
A term is alway equal to itself, this is given by the reflexivity operator (refl or r(a)) like this:
Or more formally: from ncatlab (hypothetical form):
from Warren:
rA(a) is the reflexitivity term for 'a' |
||||||||
| term elimination |
then we can construct a canonically defined term J(t;x,y,p):C(x,y,p) for any x, y, and p:Id A(x,y), by “transporting” the term t along the proof of equality p. |
from ncatlab:
from Warren:
J is the elimination term B is type representing identity variable 'u' gets bound, indicated by square brackets. |
||||||||
computation rule β-reduction |
We can substitute along a reflexitivity proof without changing it. |
|
||||||||
| coherence or "Beck-Chevalley" rules | ||||||||||
Reflexitivity does not fully define equality, for example ≥is reflexive but is not the same as =. The eliminator 'J' is the 'least reflexive relation' that is, only types on the diagonal are inhabited, this is its universal property (extreemal clause).
If the types which are not on the diagonal are not inhabited we can say anything about them, so we need a function going in the other direction (the eliminator).
J=Q[M/a]
Definitional Equality (Judgmental Equality) |
Propositional Equality (Identity Equality) |
|
|---|---|---|
The equality used when making a definition: f(x) = x |
The equality you use when stating a proposition to be proved: x = x + 0 |
|
| For instance the symbols “2” and “s(s(0))” (meaning the successor of the successor of 0) are definitionally/intensionally equal terms (of type the natural numbers): the first is merely an abbreviation for the second | ||
| written | x ≡ y | x =A y short for- x : A = y : A |
|
|
|
it 'controls type-checking'. if a:A, and A≡B , then a:B. |
if only p:A=B, then instead of a:B we have Suppose that P is a type family over A and that p:x =A y. Then there is a function p*: P(x)->P(y). |
|
| inferred automatically by the type checker | a type with corresponding term formers | |
The propositional equality type, containing proofs of equality between x and y . Here x and y must have the same type A , and if we have A : Typei , then we also have x ≡ y : Typei. |
||
| introduction rule | reflexivity refl : { A : Typei } -> ( x : A ) -> x ≡ x |
|
| equality eliminator | traditionally called J J : { A : Typei } -> ( P : ( x y : A ) -> x ≡ y -> Typej ) -> (
|
|
| computation rule | ||
Computer Code
To try to understand the equality eliminator 'J' here is some code:
Idris CodeFrom Philip Dorrell s github repository where a postulated '~~' identity type is equivalent in what it implies to the built in Idris '=' identity type. No constructor given. We would expect refl_ to be the implementation of ~~ but instead it is another undefined function. |
infix 40 ~~
postulate (~~) : t -> t -> Type
postulate refl_ : (a:t) -> a ~~ a
postulate J : (P : (a,b:t) -> (a~~b) -> Type) ->
((a:t) -> P a a (refl_ a)) ->
((a,b:t) -> (p:a~~b) -> P a b p) |
Agda Codefrom Univalence From Scratch by Martin Escardo |
J : {𝓤 𝓥 : Universe} {X : 𝓤 ̇}
-> (A : (x y : X) -> Id x y -> 𝓥 ̇)
-> ((x : X) -> A x x (refl x))
-> (x y : X) (p : Id x y) -> A x y p
J A f x .x (refl .x) = f x |
For more information Idris and proof assistants see these pages:
Extensional Equality vs. Intentional Equality
Intentional Equality |
Extensional Equality |
|||||||
|---|---|---|---|---|---|---|---|---|
| Equality | Intentional equality equates things if they are constructed in the same way. |
Extensional equality equates things that behave the same. |
||||||
| example | a+b not equal to b+a |
|||||||
| type theory | ITT | ETT | ||||||
| properties | Program always has normal form. | Allows programs that may be non-terminating. | ||||||
only proof of Id is refl |
The first form of extensional type theory (ETT) assumes types form a 'homotopy set' that is each type is a distinct point (see Oregon Programming Languages Summer School 2012 type theory part 5). HoTT takes this futher by allowing higher layers, types can be equal in multiple ways which gives a groupoid structure.
Examples
Example 1
| Start with 2 types, Int and Bool, this allows us to generate other types: | 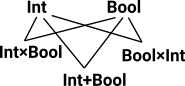 |
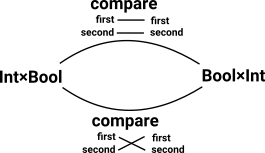 |
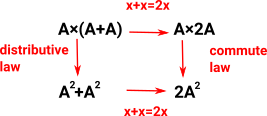
So, for instance, is Int ×Bool = Bool×Int ? Conventionally no because (3,true) ≠ (true,3) but Int ×Bool is isomorphic to Bool×Int. In HoTT we can express this isomorphism as representing equality in potenially many ways: |
Example 2
| Constructor contains proofs they are equal: | 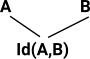 |
 |
Information content of Terms
This may not be a formal part of type theory but informally we often think about concepts like η-reduction (tells us how to simplify a term that involves a constructor applied to an eliminator) in terms of not introducing new information.
| Type | Infomation Content of Term | |
|---|---|---|
| Unit | 0 bits | |
| Product A B | Add together information in A and B |  |
| Sum A B | eliminator removes information uses energy |
 |
Category Theory - Ends and Dinatural Transformations
Equality of Dependent TypesSo how do we define equality of dependent types? On this page we look at some of the issues involving varous type of 'equalities' of types. |
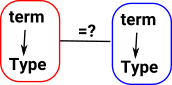 |