Logic is a language for reasoning.
On these pages I am mostly concerned with mathematical logic and the mathematical structures that are related to it. There are a common set of lattice-like structures that occur in various branches of mathematics such as orders, logic and sets.
| Order | Logic | Set | |
|---|---|---|---|
| T | top | true | universe |
| _|_ | bottom | false | Ø |
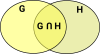
| /\ (conjunction) | greatest lower bound | and |  |
| \/ (disjunction) | least upper bound | or | U |
Logic
We often write a rule in logic like this: |
|
We take this to mean that, if all the things above the line are true, then the thing below the line is true.
Constants
Values have two values ether true of false, we may use alternative names as follows:
| true | 1 |
T | |
| false | 0 |
 |
In boolean algebra every value evaluates to either true or false. In intuitionistic logic or constructive logic a value may be neither true or false, it is only true or false when proven to be true or proven to be false.
Connectives
| conjunction | /\ | and | (boolean,boolean) -> boolean |
| disjunction | \/ | or | (boolean,boolean) -> boolean |
| negation | ¬ | not | boolean -> boolean |
| implication | ==> | if | (boolean,boolean) -> boolean |
| equivalence | <=> | if and only if (iff) | (boolean,boolean) -> boolean |
Quantifiers
 |
for all |
 |
there exists (for some) |
Propositional, FOL and HOL
| Propositional Logic | Has connectives:
Propositions could be seen as questions about set membership, for example, x is a member of X since we can construct X as a set with the property we want. |
||
| First Order Logic | Extends Propositional Logic so it has connectives plus:
Predicates act like functions that take an input value and produce a true/false value. |
||
| Higher Order Logic | As First Order Logic plus:
|
Boolean Algebra
| A | B | ¬A | ¬B | or | and | xor | A ==> B | A <=> B |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
Laws
| identity | and | or |
|---|---|---|
| commutativity | x /\ y = y /\ x | x \/ y = y \/ x |
| associativity | (x /\ y) /\ z = x /\ (y /\ z) | (x \/ y) \/ z = x \/ (y \/ z) |
| idempotency | x /\ x = x | x \/ x = x |
| absoption laws | x \/ (x /\ y) = x | x /\ (x \/ y) = x |
| distribution | (x \/ y) /\ z = (x /\ z) \/ (y /\ z) | |
| excluded middle | x /\ ¬x = false | x \/ ¬x = true |
| De Morgan (duality principle) |
¬(x /\ y) = ¬x \/ ¬y | ¬(x \/ y) = ¬x /\ ¬y |
| double negation | ¬¬x = x | |
| true and false | x /\ true = x |
x \/ true = true x \/ false = x ¬false = true |
Canonical Form
| minterm form | ¬A¬B ƒ(00) + ¬AB ƒ(01) + A¬B ƒ(10) + AB ƒ(11) |
| maxterm form | (¬A + ¬B + ƒ(00) )( ¬A + B + ƒ(01) )( A + ¬B + ƒ(10) )( A + B + ƒ(11)) |
example: exclusive or is:
Σ(1,2)=∏(0,3)
Karnaugh Maps
| A\B | 0 | 1 | |||||||||||||||||||||||||||||||||||
| EF\CD | EF\CD | ||||||||||||||||||||||||||||||||||||
| 0 |
|
|
|||||||||||||||||||||||||||||||||||
| EF\CD | EF\CD | ||||||||||||||||||||||||||||||||||||
| 1 |
|
|
Logic and Computing
There is a deep connection between: λ-calculus, intuitionistic logic and cartesian closed categories.
Curry-Howard Correspondence
There is a relationship between computer programs and mathematical proofs, this is known as the Curry-Howard correspondence.
A type in λ-calculus has the same mathematical structure as a proposition in intuitionistic logic.
A constructor for that type corresponds to a proof of the proposition. The following table has some specific types with their corresponding propositions:
| Proposition | Type |
|---|---|
| true formula | unit type |
| false formula | empty type |
| implication | function type |
| conjunction | product type |
| disjunction | sum type |
| universal quantification | generalised product type (Π type) |
| existential quantification | generalised sum type (Σ type) |
For more information about the Curry-Howard correspondence see the page here.
Computation, Logic and Geometry
Venn diagrams show us a deep connection between sets , logic and geometry. If we swap from sets to types and and from Boolean logic to constructive logic we get similar mathematical structure that has this 3-way correspondence. |
 |
| Type Theory | Logic | Geometry | |
|---|---|---|---|
| types |
|
|
|
| terms |
constants, variables & functions. |
a term is a proof of the proposition. |
|
| non-dependant types | empty |
false | initial object |
| unit T | true | terminal object | |
| sum | or | coproduct | |
| pair | and | product | |
| function | implication | internal hom | |
| dependant types | type family | predicate | bundle |
| substitution | substitution | pullback of a bundle | |
| Σ type | exists | total space of a bundle | |
| Π type | for all | space of sections of bundles |
simply typed λ-calculus
where:
- x,y... (lower case) = variables
- A,B ... (upper case, beginning alphabet) = types
- M,N ... (upper case, middle alphabet) = metavariables for terms
Formation rules for well typed terms (wtt):
- every variable x:A is a wtt.
- if x:A is a variable and M:B is a wtt then λ x:A.M: A->B is a wtt
- if M:A -> B is a wtt and N:A is a wtt then M N: B is a wtt
- if M:A is a wtt and N:B is a wtt then <M,N>: A×B is a wtt
- if M:A×B is a wtt then fst(M): A is a wtt
- if M:A×B is a wtt then snd(M): B is a wtt
Given a wtt M:B the set FV(M) of the free variables of M, is defined as follows:
- if M=x, then FV(M) = {x}
- if M=λ x:A.N, then FV(M) = FV(N)-{x}
- if M=N P, then FV(M) = FV(N) U FV(P)
- if M=<N,P>, then FV(M) = FV(N) U FV(P)
- if M=fst(N), then FV(M) = FV(N)
- if M=snd(N), then FV(M) = FV(N)
The substitution [M/x]N:B of a proof M:A for a generic x:A in a proof N:B is defined in the following way:
- if N:B = x:A then [M/x]N:B = M:A
- if N:B = y:A,x≠y then [M/x]N:B = N:B
- if N:B = λ x:C.P:B then [M/x]N:B = λ x:C.P:B
- if N:B = λ y:C.P:B,x≠y,y∉FV(M) then [M/x]N:B = λ y:C.[M/x]P:B
- if N:B = P Q then [M/x]N:B = [M/x]P[M/x]Q:B
- if N:B = <P,Q> then [M/x]N:B = <[M/x]P[M/x]Q>:B
- if N:B = fst(P) then [M/x]N:B = fst([M/x]P)
- if N:B = snd(P) then [M/x]N:B = snd([M/x]P)
Reduction - rewriting system
- α-reduction: λ x:A.M = λ y:A.[y/x]M
- β(->)-reduction: (λ x:A.M)N = [N/x]M
- η(->)-reduction: λ x:A.(M x) = M, if x∉FV(M)
- β(×)-reduction: fst(<M,N>) = M
- β(×)-reduction: snd(<M,N>) = N
- η(×)-reduction: <fst(P),snd(P)>) = P
where:
= : minimal congruence relation
