On this page is information about my code for various logic related structures including partial order, lattice structures and logic operations based on them. Logic operations based on lattice structures.
There are a common set of lattice-like structures that occur in various branches of mathematics such as orders, logic and sets. I would like to represent these structures in FriCAS.
| Order | Logic | Set | |
|---|---|---|---|
| T | top | true | universe |
| _|_ | bottom | false | Ø |
| /\ (conjunction) | greatest lower bound | and |  |
| \/ (disjunction) | least upper bound | or | U |
What I have done so far seems to be applicable to finite lattices but a lot of my interest in this subject would be infinite structures. Especially structures from Topology such as a 'frame' which is a complete lattice with infinite meets. I am also interested in structures from computer science such as domain theory.
Posets and Lattices
Finite lattices may be based on a poset (partial order).
My strategy so far is to have two sorts of domains:
- posets - here the representation is the whole structure.
- lattices - here the representation is an element of the structure.
So for the poset, the representation would be the whole structure, like this:
Rep := Record(set:List S,struct:List List Boolean)
The lattice is an algebraicizing of this. The lattice type constructor would take the poset as a parameter.
A Partially Ordered Set (POSET) is a structure with an operator '<=' with a binary
output:
<=(a:%,b:%) -> Boolean
This structure has the following axioms:
- reflexivity
l(x): x<=x - antisymmetry(x,y): x<=y and y<=x iff x=y
- transitivity(x,y,z): x<=y and y<=z implies x<=z
| Overview of main posets: |  |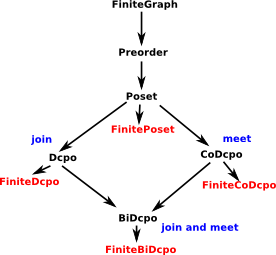
| key: | black=category | red=domain | blue=axioms |
A lattice is the same structure (every lattice is a poset, not every poset is a
lattice) but it is an algebra (in the universal algebra sense) which has binary
operations:
- x \/ y
- x /\ y
Which obey the following axioms:
| commutativity(x,y): |
x \/ y=y \/ x | x /\ y=y /\ x |
| associativity(x,y,z): |
(x \/ y) \/ z=x \/ (y \/ z) | (x /\ y) /\ z=x /\ (y /\ z) |
| idempotencex: |
x \/ x=x | x /\ x=x |
Both of these forms could probably be crunched together in the same FriCAS
category/domain. The approved Axiom/FriCAS style seems to be to include as
many functions as possible in categories/domains rather than separating them
out.
However we need to use these structures differently so my strategy so far is
to have two sorts of domains:
- posets - here the representation is the whole structure.
- lattices - here the representation is an element of the structure.
So for the poset, the representation would be the whole structure, like this:
Rep := Record(set:List S,struct:List List Boolean)
The lattice is an algebraicizing of this. The lattice constructor would take the poset
as a parameter. So corresponding poset and lattice categories are shown in the following table:
| Poset Categories | Lattice Categories |
|---|---|
| Poset | |
| Dcpo | JoinSemilattice |
| CoDcpo | MeetSemilattice |
| BiCPO | Lattice |
Overview of main lattice categories and domains: (Modified as suggested by Waldek on thread here) |
 |
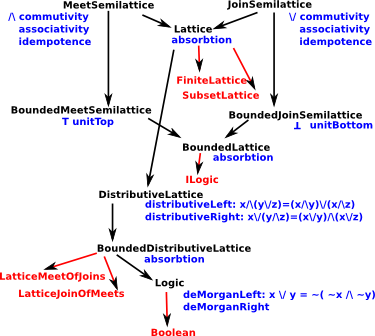| key: | black=category | red=domain | blue=axioms |
In practice Boolean would not really extend Poset but I was thinking of a more general type of logic which could be defined from a diagram like this:
| Boolean |  |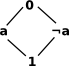
A Boolean algebra is a full lattice where a \/ ¬a is 1 (true) |
| Heyting |  |
This does not apply for Heyting algebra, that is no: 'Law of excluded middle' |
Poset and Lattice Definitions
A lattice is an algebraicizing of a poset by defining it in terms of a binary meet and join operator.
Here we will define two types of 'lattice' and 'semilattice'
- Bounded Lattice: have the requirement that a unique 'top' and 'bottom' exists. So not every poset will give rise to a valid lattice but every lattice has a corresponding poset.
- Unbounded Lattice: do not have the requirement that a unique 'top' and 'bottom' exists. For finite lattices, top and bottom will exist since we can do a meet/join of all values (meet and join are not partial functions)
| Here x and y are shown as having two possible meets but this would not be a valid lattice since the result of the meet operation must be unique. |  |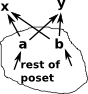
 |
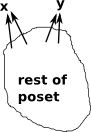Even if individual meets are unique this poset would still not be valid because the top element is not unique. |
| We could try connecting 'x' and 'y' to make them both top elements, but this does not work, because by antisymmetry x and y must be equal. So there must be one unique top element. |  |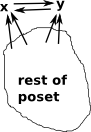
In addition to these mathematical differences between posets and lattices there is also a big differences in the way that they are implemented as domains in the program in that the representation is different:
- posets - here the representation is the whole structure.
- lattices - here the representation is an element of the structure.
So for the poset, the representation would be the whole structure, like this:
Rep := Record(set:List S,struct:List List Boolean)
A poset is then used in the type constructor for a corresponding lattice domain.
Functions from poset to poset
- preserves meets
- preserves joins
- preserves implication
Closure operators
An endofunction cl: P -> P from a poset P to itself is called a closure operator if it satisfies the following:
- Axiom extensive:(x): x <= cl(x)
- Axiom increasing:(x,y):x <= y implies cl(x) <= cl(y)
- Axiom idempotent:(x):cl(cl(x)) = cl(x)
A fixpoint of the function cl, i.e. an element c of P that satisfies cl(c) = c, is called a closed element. A closure operator on a partially ordered set is determined by its closed elements.
Any partially ordered set P can be viewed as a category, with a single morphism from x to y if and only if x <= y. The closure operators on the partially ordered set P are then the monads on the category P.
[ref 4]
Relationship to Existing Code
There is already some poset and lattice related code as listed here:
- Related packages: UserDefinedPartialOrdering in setorder.spad
- Related categories:
- PartialOrder in catdef.spad
- Logic and Boolean in boolean.spad
- Related domains: DirectedGraph in graph.spad
I have also moved intuitionistic logic 'ILogic' from computation.spad to here.
The aim is to generalise, extend and put all this code together.
Category Preorder
Has <=(%,%) -> Boolean operation together with the following axioms:
- reflexivity(x): x<=x
- transitivity(x,y,z): x<=y and y<=z implies x<=z
Domain Poset
Description: Preorder with antisymmetry axiom. Holds a complete set together with a structure to codify the partial order.
Axioms:
- reflexivity(x): x<=x
- antisymmetry(x,y): x<=y and y<=x implies x=y
- transitivity(x,y,z): x<=y and y<=z implies x<=z
This holds a complete set together with a structure to codify the partial order. The elements are put in a list so they can be enumerated and linked to the structure. The structure is a two dimensional array to determine: is each element is connected to each other element.
More documentation for poset code on page here.
MeetSemilattice and BoundedMeetSemilattice
Implementations include regressive inner, meet product operator. Need to check precedence when used as an infix operator.
Axioms:
- commutativity(x,y): x /\ y=y /\ x
- associativity(x,y,z): (x /\ y) /\ z=y /\ (x /\ z)
- unitx
T: x /\ T =x ................ for bounded only - idempotencex: x /\ x=x
JoinSemilattice and BoundedJoinSemilattice
This is different from exterior Grassmann product operator because that anticommutes. Need to check precedence when used as an infix operator.
Axioms:
- commutativity(x,y): x\/y=y\/x
- associativity(x,y,z): (x\/y)\/z=y\/(x\/z)
- unitx_|_: x \/ _|_ =x ................ for bounded only
- idempotencex: x\/x=x
JoinSemilattice: Category == SetCategory with _\_/: (%, %) -> % ++ returns the logical 'join', e.g. 'or'.
Lattice and BoundedLattice
Combines Meet and Join Semilattices.
Axioms:
- absorptionMeetOverJoin(x,y): x/\(x\/y)=x
- absorptionJoinOverMeet(x,y): x\/(x/\y)=x
DISTLAT DistributiveLattice and BoundedDistributiveLattice
Not every lattice is distributive so treat this as a different case.
Axioms:
- distribution1(x,y,z): x/\(y\/z)=(x/\y)\/(x/\z)
- distribution2(x,y,z): x\/(y/\z)=(x\/y)/\(x\/z)
In addition to the DistributiveLattice category, I have included special domains:
- LatticeMeetOfJoins
- LatticeJoinOfMeets
which encode distributive lattices more efficiently, they are explained on the page here.
FRAME Frame
Description: frames are used in topology and are the lattice associated with the concept of a 'locale'. see: [1]
A Frame is a Lattice where certain subsets are also Lattices.
The general case of these examples are recursively defined types.
I cannot work out how to represent infinite conjunctions, we could supply a list of arguments like this:
join(elements:List(%)):% ==
but to encode the important structure we need to take the limit as the number of arguments approaches infinity. So I suspect we need to use some sort of infinite series.
I don't know how to go about this so, for now, I have removed my attempts to encode a frame structure.
More about frames on page here.
FiniteLattice
This is the algebration of poset. A big difference between this lattice domain and the poset domain is that, in this domain, the REP holds a single node whereas in poset REP holds the whole poset.
Example Session 1
As an example I will create a poset like the one illustrated on the right: After that we will go on to do lattice operations on it. |
 |
 |
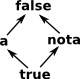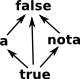This does not yet obey the transitivity law so we need to add an arrow as on the left. Although, for simplicity, such transitive completion is not always shown in diagrams. |
| Similarly we need to obey the reflexivity law. So I have applied reflexivity completion here: |  |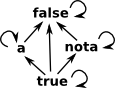
So first we create the nodes:
(1) -> objs := ["false","a","nota","true"]
(1) ["false","a","nota","true"]
Type: List(String)
| We now need to encode the arrows as a table like this: |
|
||||||||||||||||||||||||||||||||
(2) -> arr := [[true,true,true,true],[false,true,false,true], [false,false,true,true], [false,false,false,true]]
(2)
[[true,true,true,true], [false,true,false,true], [false,false,true,true],
[false,false,false,true]]
Type: List(List(Boolean))
We can now create the poset:
(3) -> pset := poset(objs,arr)
+true true true true+
| |
|false true false true|
(3) | |
|false false true true|
| |
+false false false true+
Type: Poset(String)
We now need to go on and calculate various lattices
(4) -> FL := FiniteLattice(String,pset)
(4)
FiniteLattice(String,[[true,true,true,true],[false,true,false,true],[false,fa
lse,true,true],[false,false,false,true]])
Type: Type
(5) -> a := finiteLattice("a")$FL
(5) "a"
Type: FiniteLattice(String,[[true,true,true,true],[false,true,false,true],
[false,false,true,true],[false,false,false,true]])
(6) -> b := finiteLattice("nota")$FL
(6) "nota"
Type: FiniteLattice(String,[[true,true,true,true],[false,true,false,true],
[false,false,true,true],[false,false,false,true]])
(7) -> a /\ b
(7) "false"
Type: FiniteLattice(String,[[true,true,true,true],[false,true,false,true],
[false,false,true,true],[false,false,false,true]])
(8) -> a \/ b
(8) "true"
Type: FiniteLattice(String,[[true,true,true,true],[false,true,false,true],
[false,false,true,true],[false,false,false,true]])
Example Session 2
| In this example we want to generate a lattice of a powerset. |  |
(1) -> ps := powerset(["a","b","c"])$PosetFactory(String)
+true false false false false false false false+
| |
|true true false false false false false false|
| |
|true false true false false false false false|
| |
|true true true true false false false false|
(1) | |
|true false false false true false false false|
| |
|true true false false true true false false|
| |
|true false true false true false true false|
| |
+true true true true true true true true +
Type: Poset(List(String))
(2) -> FL := FiniteLattice(List(String),ps)
(2)
FiniteLattice(List(String),[[true,false,false,false,false,false,false,false],
[true,true,false,false,false,false,false,false],[true,false,true,false,false,
false,false,false],[true,true,true,true,false,false,false,false],[true,false,
false,false,true,false,false,false],[true,true,false,false,true,true,false,fa
lse],[true,false,true,false,true,false,true,false],[true,true,true,true,true,
true,true,true]])
Type: Type
(3) -> z := finiteLattice([])$FL
(3) []
Type: FiniteLattice(List(String),[[true,false,false,false,false,false,false,false],
[true,true,false,false,false,false,false,false],[true,false,true,false,false,false,false,false],
[true,true,true,true,false,false,false,false],[true,false,false,false,true,false,false,false],
[true,true,false,false,true,true,false,false],[true,false,true,false,true,false,true,false],
[true,true,true,true,true,true,true,true]])
(4) -> a := finiteLattice(["a"])$FL
(4) ["a"]
Type: FiniteLattice(List(String),[[true,false,false,false,false,false,false,false],
[true,true,false,false,false,false,false,false],[true,false,true,false,false,false,false,false],
[true,true,true,true,false,false,false,false],[true,false,false,false,true,false,false,false],
[true,true,false,false,true,true,false,false],[true,false,true,false,true,false,true,false],
[true,true,true,true,true,true,true,true]])
(5) -> b := finiteLattice(["b"])$FL
(5) ["b"]
Type: FiniteLattice(List(String),[[true,false,false,false,false,false,false,false],
[true,true,false,false,false,false,false,false],[true,false,true,false,false,false,false,false],
[true,true,true,true,false,false,false,false],[true,false,false,false,true,false,false,false],
[true,true,false,false,true,true,false,false],[true,false,true,false,true,false,true,false],
[true,true,true,true,true,true,true,true]])
(6) -> c := finiteLattice(["c"])$FL
(6) ["c"]
Type: FiniteLattice(List(String),[[true,false,false,false,false,false,false,false],
[true,true,false,false,false,false,false,false],[true,false,true,false,false,false,false,false],
[true,true,true,true,false,false,false,false],[true,false,false,false,true,false,false,false],
[true,true,false,false,true,true,false,false],[true,false,true,false,true,false,true,false],
[true,true,true,true,true,true,true,true]])
(7) -> a /\ b
(7) ["a","b"]
Type: FiniteLattice(List(String),[[true,false,false,false,false,false,false,false],
[true,true,false,false,false,false,false,false],[true,false,true,false,false,false,false,false]
,[true,true,true,true,false,false,false,false],[true,false,false,false,true,false,false,false],
[true,true,false,false,true,true,false,false],[true,false,true,false,true,false,true,false],
[true,true,true,true,true,true,true,true]])
(8) -> a /\ b /\ c
(8) ["a","b","c"]
Type: FiniteLattice(List(String),[[true,false,false,false,false,false,false,false],
[true,true,false,false,false,false,false,false],[true,false,true,false,false,false,false,false],
[true,true,true,true,false,false,false,false],[true,false,false,false,true,false,false,false],
[true,true,false,false,true,true,false,false],[true,false,true,false,true,false,true,false],
[true,true,true,true,true,true,true,true]])
(9) ->
Future Enhancements
Implementation of Proof
It would be good to implement a proof as a tree.
Next Steps
I have put some further detail on these pages:
Or for related topics see these pages:
Or some Pages about the theory:
References
For more details see:
- [1] Topology Via Logic - Steven Vickers ISBN 0 521 57651 2
Steven Vickers -
Topology Via Logic. - [2] J. Lambek, P. J. Scott 1988
Introduction to Higher-Order Categorical Logic ISBN : 0521356539
This book shows the relationship between mathematical logic and category
theory. Introduction to Higher Order Categorical Logic - Lambek & Scott - Relates lambda calculus to higher order logic and cartesian closed categories.
- [3] Automated Lattice Drawing: Ralph Freese http://www.math.hawaii.edu/~ralph/Preprints/latdrawing.pdf
- [4] wikipedia closure operator: https://en.wikipedia.org/wiki/Closure_operator
- [5] http://math.stackexchange.com/questions/174475/kleisli-category-examples
