So far I have only implemented cell complexes and in particular simpectial complexes as representations of topology. It is my intention to relate this to other representations of topology such as (co)homotopy groups and homology.
Cell Complexes
There are many ways to approach cell complexes. They originally arose from topology but they can also be used in a purely combinatorial context or an algebraic context. We can also look at them as a greneralisation of the structure of a graph. |
Graph: |
Simpectial Complexes
| In a graph an edge has arrows to two vertices (the source and target). Simpectial complexes generalise this to allow any number of vertices. |  |
A 'simplex' is a set of vertices such that every subset is included in the simplex. For example a tetrahedron contains all its faces and lines.
A 'simplicial complex' is a set of these simplexes which may have vertices in common.
Because each simplex contains its subsets this is a combinatorial structure, when used in this way the structure is known as an 'abstract simplicial complex' optionally we can also associate a point in a space with each vertex, in this case the structure is known as an 'geometric simplicial complex' and it has geometric/topological/homotopy properties.
See this page for more details.
Delta Complexes
| We represent the complex as a sequence of 'face maps' each one indexed into the next. |
This is an alternative way to represent simpectial complexes, in most (but not all) cases the representations are isomorphic
See this page for more details.
Homotopy
A homotopy is a continuous mapping between two spaces. Often parameterised by 't' to be though of as time.
See this page for more details.
Homotopy Groups
The fundamental group of a pointed space (mostly represented here by simpectial complexes) is isomorphic to the fundamental group of the space (Seitert-Van Kampen theorem).
We look at loops of maps from a point to the given space. Each loop, in the space, from the point back to itself is a generator for the group. These loops can then be composed. The homotopy group is is finitely presented by generators and relations. This representation of a group is not, in general, algorithmically computable into other representations of a group. |
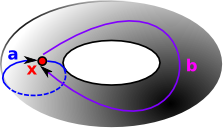 |
| The simplest homotopy group is the fundamental group. It determines when two paths, starting and ending the point, can be continuously deformed into each other. It records information about the shape in terms of holes in the topological space. | 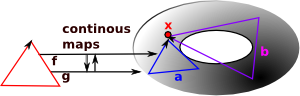 |
| nth homotopy group. Instead of mapping a circle onto our topological space we map a sphere or higher order sphere onto the space. | 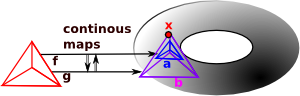 |
To generate the fundamental group from the simplicial complex see the page here.
Homology
| When we looked at the delta complex we got a chain of 'face maps' between each dimension and the next lower one. |  |
In homology we treat this as a chain of abelian groups.
I have gone into more detail on the page here.
Examples of Complexes
Here are some examples generated by the FriCAS program. There is a 'factory' domain to generate common simplexes:
FACTORY:=SimplicialComplexFactory(Integer)
(1) SimplicialComplexFactory(Integer)
Type: Type |
First we define a shorter name for SimplicialComplexFactory. |
The type parameter is only used when generating cohomology. We use 'Integer' but this is not relavent here.
Band - Cylinder without ends: (2) -> band()$FACTORY
(2) points 1..6
(1,2,3)
(1,2,6)
(1,5,6)
(2,3,4)
(3,4,5)
(4,5,6)
Type: FiniteSimplicialComplex(Integer)
|
Two boundaries, shown in red and blue: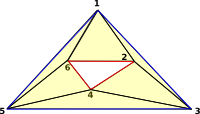 |
Torus - (3) -> torusSurface()$FACTORY
(3) points 1..7
(1,2,3)
(2,3,5)
(2,4,5)
(2,4,7)
(1,2,6)
(2,6,7)
(3,4,6)
(3,5,6)
(3,4,7)
(1,3,7)
(1,4,5)
(1,4,6)
(5,6,7)
(1,5,7)
Type: FiniteSimplicialComplex(Integer)
|
No boundaries, the red arrows at the top and bottom join up and the blue arrows on the left and right join up. 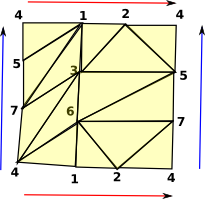 |
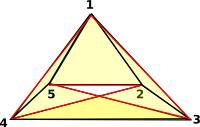
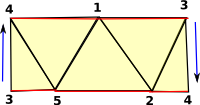
Möbius band: One boundary, shown in red: (4) -> moebiusBand()$FACTORY
(4) points 1..5
(1,2,3)
(2,3,4)
(3,4,5)
(1,4,5)
(1,2,5)
Type: FiniteSimplicialComplex(Integer) |
This diagram can only be realised in 3D, to make it clearer in 2D I have duplicated nodes 3 and 4:
The blue arrows should join up, notice the head of the arrow is at the top on the left and bottom on the right. |
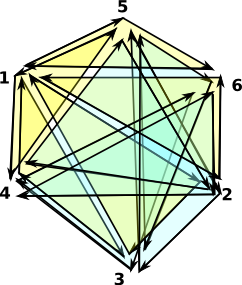
Projective Plane - No boundaries, every edge is connected to two faces: (5) ->projectiveSpace(2)$FACTORY
(5) points 1..6
(1,2,3)
(1,3,4)
(1,2,6)
(1,5,6)
(1,4,5)
(2,3,5)
(2,4,5)
(2,4,6)
(3,4,6)
(3,5,6)
Type: FiniteSimplicialComplex(Integer)
|
Above is my attemp to draw, with each vertex appearing once, this makes the diagram very cluttered and hard to understand. Its easier to draw if nodes 4,5 and 6 appear twice as below:
Note: edges 4->5, 5->6 and 6->4 connect two faces but they wind in the same direction. |