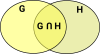
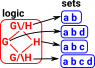
Algebraic topology links topology and algebra, for instance, it can turns topology problems into algebra problems. First lets think about the ways that these subjects may be related:
Sets, Logic and Topology
Venn diagrams |
Venn diagrams give a very intuitive way to look at sets and their intersections and unions. It is a first step to showing a deep and beautiful link between sets (union, intersection), logic (and, or) and topology. There is a problem with Venn diagrams, they do not work so well when we increase the number of sets. Its alright with 3 sets, we can draw 3 circles showing all possible intersections, but its more difficult with 4 or more sets. |
Logic LatticesTo have a diagram that scales up to many sets it seems to be necessary to separate the sets from the logic. This diagram is less intuitive and compact than Venn diagrams but it is still very powerful. It must obey certain axioms so that the sets are consistent with the logic part. For more information see the page about sheaves. |
 |
There are other links between topology and algebra. Here we will look at an equivalence between spaces and groups:
Topological Equivalence.
As discussed on an earlier page, in two dimensions it is relatively easy to determine if two spaces are topologically equivalent (homeomorphic). We can check if they:
- are connected in the same way.
- have the same number of holes.
However, when we scale up to higher dimensions this does not work and it can become impossible to determine homeomorphism. There are methods which will, at least, allow us to prove more formally when topological objects are not homeomorphic.
These methods use 'invariants': properties of topological objects which do not change when going through a homeomorphism.
| An important invariant is the number of 'holes' in each dimension. | 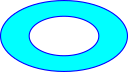 Here there is one hole, any homeomorphic transformation will still have one hole. |
| Dually we could look at the maximum number of n-dimensional cuts we can make without dividing into two. This is really the same thing since each cut removes a hole. | 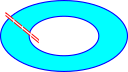 This cut does not divide the shape into two parts because we can still go round the other way. |
If the above invariants are the same it is a good indication that the shapes are homeomorphic but it is not enough, other factors like 'torsion' also need to be unchanged to be sure.
Here we look at two types of invariants which arise from homotopy and homology. (I have written some code to implement these structures on the page here)
These invariants can be expressed as algebraic structures, particularly groups, so this subject is called 'algebraic topology'. The way that these algebraic structures arise is discussed on the homotopy and homology pages but first we need to introduce a way to specify topological objects in a way that we can calculate with. We will do this by using simplicial complexes.
Equivalance Classes
Equivalance classes exist when we have classes we wish to consider essentially the same.
Examples:
- A set of objects with the same shape.
- The set of integers with the same remainder when divided by a given number.
So we can start to get the idea that this is related to the concept of quotient.
An equivalence relation has the following properties:
- reflexive
- symmetric
- transitive
See partial order for more.
Homotopy and Homology Equivalance
In the homotopy case we have path components of X written π(X)
 |
We have a continuous map from space X to space Y: f: X -> Y and a continuous map from space Y to space X: g: Y -> X |
| Homotopy | Homomorphism |
|---|---|
A homotopy equivalence is where the composition: g o f: X -> X is homotopic to the identity map on X and simlarly for: f o g: Y -> Y |
A homomorphism is where the composition: g o f: X -> X is equal to the identity map on X and simlarly for: f o g: Y -> Y |
Homotopy
A homotopy is a continuous mapping between two spaces. Often parameterised by 't' to be though of as time.
Homotopy Groups
The fundamental group of a pointed space (mostly represented here by simpectial complexes) is isomorphic to the fundamental group of the space (Seitert-Van Kampen theorem).
We look at loops of maps from a point to the given space. Each loop, in the space, from the point back to itself is a generator for the group. These loops can then be composed. The homotopy group is is finitely presented by generators and relations. This representation of a group is not, in general, algorithmically computable into other representations of a group. |
 |
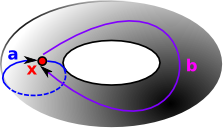The simplest homotopy group is the fundamental group. It determines when two paths, starting and ending the point, can be continuously deformed into each other. It records information about the shape in terms of holes in the topological space. |
 |
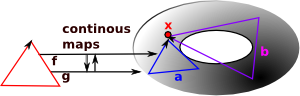nth homotopy group. Instead of mapping a circle onto our topological space we map a sphere or higher order sphere onto the space. |
 |
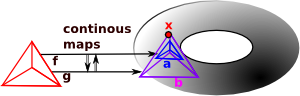To generate the fundamental group from the simplicial complex see the page here.
Homology
When we looked at the delta complex we got a chain of 'face maps' between each dimension and the next lower one. |
 |
In homology we treat this as a chain of abelian groups.
More detail on the page here.
Cell Complexes
There are many ways to approach cell complexes. They originally arose from topology but they can also be used in a purely combinatorial context or an algebraic context. We can also look at them as a greneralisation of the structure of a graph. |
 |
Cell Complexes
In a graph an edge has arrows to two vertices (the source and target). Simpectial complexes generalise this to allow any number of vertices. |
 |
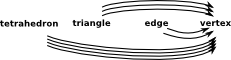A 'simplex' is a set of vertices such that every subset is included in the simplex. For example a tetrahedron contains all its faces and lines.
A 'simplicial complex' is a set of these simplexes which may have vertices in common.
Cell complexes are described on this page.
Next Steps
- The additional tests for a geometric simplicial complex are described on the page here.
- The way we implement topological aspects of simplicial complexes such as boundaries and cycles is explained on the page here.
- To generate the fundamental group from the simplicial complex see the page here.
- Products are quite complicated so I have put this on a separate page here.
Bibliography
For more details see:
- [1] Mathematics++ Kantor,Matousek,Samal 2015 ISBN 978-1-4704-2261-5 Chapter 6 - Topology. Contains a relatively gentle introduction to homology.
- [2] Graphs, Surfaces and Homology, Peter Giblin 2010 ISBN 987-0-521-15405-5
Builds up to homology groups via graphs and simplicial complexes. - [3] Wikipedia
- [4] How to compute this stuff
- [5] Hatcher - Algebraic Topology - book also available free online.
