Introduction
This page continues from the model category page here and fibration page here.
Fibration and Co-fibration
Homotopy has the concept of:
- a fibration which has the lifting property.
- a co-fibration which has the extension property -extension is dual to lift.
Fibration |
Co-fibration (Extension Property) |
|
|---|---|---|
| Homotopy | Fibration |
Co-fibration (see page here) |
Combinatorics |
Kan fibration (see page here) |
Kan extension (see page here) |
Kan fibrations are combinatorial analogs of Serre fibrations of topological spaces.
Cofibrations from Fibres
Here we introduce cofibrations by extending the concept of fibres and fibre bundles.
A fibre bundle is a set of lines/links between a base space B and a total space E. These link elements of B with, possibly multiple, elements of E. This is a continuous surjective map. This forms a space that is locally a product space, but globally may have a different topological structure (see Wikipedia page). |
 |
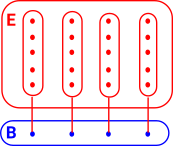So elements of B are linked to sets of elements in E. That is the surjective function P from E to B can't be exactly reversed but the nearest we can get is to map back to sets of elements.
 |
Can we take this further and treat P as a functor and map a function back along P-1 ? When we 'lift' f up to E we can't just assume that the function g will map corresponding elements:
fibrations can be more complicated and interesting than that. As shown the green arrows might go to any element. |
 |
(Co)fibration - Point to Line Map Example
In a homotopy equivalence (but not a homeomorphism) we can have continuous maps between a line and a point.
 |
For the direction from the line to the point all the points in the line map to the point A. |
| For it to be a continuous map the preimage of the open sets must be an open set. So the open set containing the point maps to an open set around the whole line. |  |
 |
For the direction from the point to the line a map f: A -> Y can only map to a single point in the line. |
 |
In order to map to the whole line we need a whole family of maps h: A×[0,1] -> Y That is a homotopy, there is a continuous mapping between the maps. |
For it to be a continuous map the preimage of the open sets must be an open set. So all the open sets in the line must map back to the open set containing the point. |
 |
This is the homotopy extension property. When we look at more complicated examples (see cofibration page) we will see a mapping to a subset can be extended to the whole set.
Homotopy Extension Property (HEP) - Example
Here is an example of a Cofibration showing the homotopy extension property (HEP)
 |
Here we have three topological shapes:
|
A is a subspace of X so the map from A to X is an injective mapping. The pair [X,A] has the HEP if certain conditions are met.
The arrow from A to Y is a homotopy h: A×[0,1] -> Y (it is a continuous family of maps from a point to a line).
 |
We also have a map F:X->Y. Because this is a single map we cant map the point to the line (bar in Θ). |
We need to be able to extend the map F:X->Y to the homotopy H: X ×[0,1] -> Y. This is what the HEP allows us to do. |
 |
As Continuous Map
 |
Here we are looking for a continuous map to map a topological space to map to something homotopy equivalent. As explained on page here a function f : X->Y is continuous if f-1(V) is open for every open set V in Y. Can we treat simplcies like open sets? So the simplcies map in the opposite direction to vertices? The simplcies may map to simplcies of a different dimension, so here the middle bar (edge) maps to a vertex. This continuous map should preserve loops, does this do that? can we prove it? |
More information:
 |
There are conditions to allow this. the arrows from A must play well with the map F. |
 |
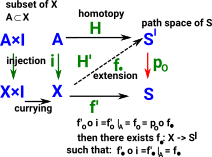Mapping Cylinder and Mapping Cone
A sort of generalised test diagram.
Extension Property in Topology
This is the inverse of the lift property. There is an injection and in this example the open sets in the other direction collapse to an open set with a single vertex. In the more general case maps from an open subset can be expanded to the whole (open) set. |
 |
For more about the extension property see the page here.
Extension as Dual to Lift.How can we get HEP by reversing the arrows in the diagram for fibrations (on the previous page)? Co-fibration involves the concept of extension
|
 |
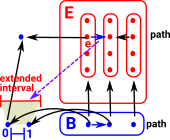| If we have a path and part of that path is specified by an interval, how do we extend that interval? |  |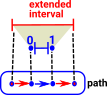
| When we inject A×I U X×0 into X×I we seem to be able to fill in the missing corner. |  |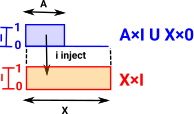
HEP in Simplicial Complex
A simplicial complex has the HEP with respect to any subcomplex. This allows homotopies to be constructed piece by piece.
simplicial complex is discussed on the page here. Each face (above dimension 0) will contain multiple sub-faces so this starts the look like a many:one relationship. |
 face maps |
 |
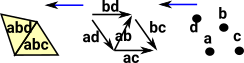However, in a complex, faces can share the same boundary so there is a many:one relationship in the opposite direction. For instance, 'ab' is contained in both 'abc' and 'abd'. |
| So the relationship between say, a triangle and a line is a many:many relationship. This can be modeled like this: | 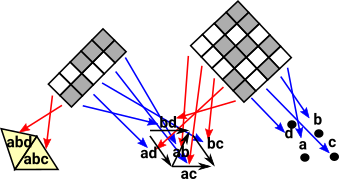 co fibre sequence |
So each of these maps is like a subset of a product.
This can be modeled using linear algebra (vector and matrix) although not quite in the usual way. Where the shapes are the vectors (just a list of subshapes) and the relationships between them are matrices. Say:
- 0 means subset relationship does not exist.
- 1 means subset relationship exists.
Next
- sheaves
- Fibrations and Cofibrations are used in model theory.
- Kan Extensions
Related Pages on this Site
