Maths - Kan Extensions - Martin Baker

Kan Extensions

Left Kan Extension	Right Kan Extension

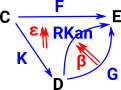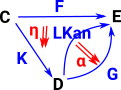
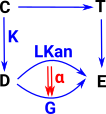
Given functors F and K the left Kan extension is a functor which closes the triangle and is unique in that it has a map to every other functor from D to E which makes the triangle commute. That is, every other functor factors through it.	Given functors F and K the right Kan extension is a functor which closes the triangle and is unique in that it has a map from every other functor from D to E which makes the triangle commute. That is, every other functor factors through it.

Examples

Example - Relational Database Join Tables

A relational database consists of tables.
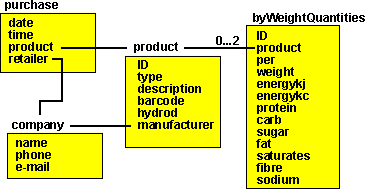If we want a many to many relationship (multiple records in a table are associated with multiple records in another table) we need to add a join table.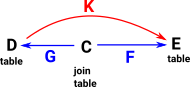

Example - Generalise Maps in Sets

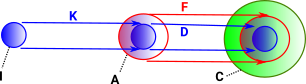
Here D,C and E are sets.

The arrows G and F are ordinary mappings between sets (that is they may be injections, surjections or bijections).

This allows us to generate an arrow K which may be a more general type of arrow. To get some intuition what this means it helps to look inside these sets and functions.

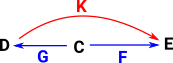In this way we can construct a new type of category with mappings where elements in the domain may map to zero or more than one elements in the codomain.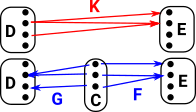

An Example Natural Numbers to Integers

Here D,C and E are natural numbers.

The arrows G and F are additions of natural numbers.

This allows us to generate an arrow K which may be a more general type of arrow which has now generated the negative numbers and so created the integers.

If we start off with natural numbers (0,1,2,3...) and we define an operation (plus) on it, by taking the inverse of this operation (subtraction) we generate the negative numbers which gives us the integers.

It is often the case that taking the inverse will generate new objects. Another example would be taking the inverse of multiplication to give rational numbers.

However we can generalise even further than inverse operations to Kan extensions.

Consider natural numbers. We can include the negative numbers but how can we extend addition so that it has the correct properties for negative numbers?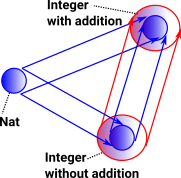

Fibration and Co-fibration

Homotopy has the concept of:

a fibration which has the lifting property.
a co-fibration which has the extension property -extension is dual to lift.

	Fibration (lifting property)	Co-fibration (Extension Property)
Homotopy	Fibration (see page here)	Co-fibration (see page here)
Combinatorics (simplicial sets)	Kan fibration (see page here)	Kan extension (see page here)

Kan fibrations are combinatorial analogs of Serre fibrations of topological spaces.

HEP and Kan Extensions

Relationship to homotopy extension principle.

If we look at the category theory diagram for the homotopy extension principle HEP (see page here).
Compare it with the diagram for the Kan extension. The above diagram appears to be a special case of the Kan extension (most things are!) so, in this diagram, 'F' is a constant mapping and 'K' is injective.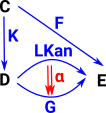
In order to make F constant we factor it through the terminal object.

Topos Theory and Kan Extensions

Relationship to topos theory.

Looking at the diagram for the sub-object classifier (see page here):

This looks similar to a special case of Kan extensions. In order to make F constant we factor it through the terminal object.

Computer Code

How can we write code to implement this?

data LKan C D E where
  LKan : (C b -> E) -> D b -> LKan C D E

Another Way to look at it

K is a functor which injects I into A
D is a functor which then injects this into C

see Bartosz Milewski blog

AGDA Code

Agda code from https://github.com/copumpkin/categories/blob/master/Categories/Lan.agda

{-# OPTIONS --universe-polymorphism #-}
module Categories.Lan where

open import Level
open import Categories.Category
open import Categories.Functor hiding (_≡_)
open import Categories.NaturalTransformation

record Lan {o₀ ℓ₀ e₀} {o₁ ℓ₁ e₁} {o₂ ℓ₂ e₂} 
           {A : Category o₀ ℓ₀ e₀} {B : Category o₁ ℓ₁ e₁} {C : Category o₂ ℓ₂ e₂}
           (F : Functor A B) (X : Functor A C) : Set (o₀ ⊔ ℓ₀ ⊔ e₀ ⊔ o₁ ⊔ ℓ₁ ⊔ e₁ ⊔ o₂ ⊔ ℓ₂ ⊔ e₂) where
  field
    L : Functor B C
    ε : NaturalTransformation X (L ∘ F)

    σ : (M : Functor B C) -> (α : NaturalTransformation X (M ∘ F)) -> NaturalTransformation L M

    .σ-unique : {M : Functor B C} -> {α : NaturalTransformation X (M ∘ F)} -> 
                (σ′ : NaturalTransformation L M) -> α ≡ (σ′ ∘ʳ F) ∘₁ ε -> σ′ ≡ σ M α
    .commutes : (M : Functor B C) -> (α : NaturalTransformation X (M ∘ F)) -> α ≡ (σ M α ∘ʳ F) ∘₁ ε

Ends

An 'end' is a generalsation of a product.

It multiplies all products together.

forall a . p a a

see Bartosz Milewski on Youtube here

Comma and Slice Categories

Also related are comma and slice category.

See this page.

Computer Code

There exists b such that:

data LKan g h a where
  LKan : (g b -> a) -> h b -> LKan g h a

where

(g b -> a) as an object of the comma category Ka
f b as the mapping of b under the functor F
b - the projection of this object back to C

where

Signature	Logic	Contains
A+B		an element of A or an element of B
(A,B) or A*B		tuple (an element of both A and B)
A -> B	AB	an element of B for every element of A
A -> B -> C -> D	A,B,CD
A -> (B -> (C -> D))		same as A -> B -> C -> D
(A, B, C) -> D		same as A -> B -> C -> D (uncurried)
(A -> B) -> C	(A->B)C	like a second level of forall on A