Mathematics and computing are linked at various levels. On these pages we look at the relationship between category theory and computing and the relationship between these and algebra. I am interested in these both:
- To try to model category theory using computer programs.
- To try to better understand programming ideas using category theory concepts.
In particular it would be interesting to see how the mathematical concept of an 'algebra' could be modeled on a computer.
Category theory and Computing
The diagram on the right represents a category with the following objects:
Note: further down the page the symbol 'Ω' Omega is used differently to represent the whole set of function signatures. In the literature you may find Ω being used for either of these things so its best to check. The 'functions' between these objects are:
|
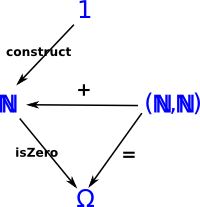 |
In a programming language we often use a construction with a set of function signatures such as those on the right, for example:
|
+(N,N)->N |
So these programming constructs appear to have the same information as a category diagram. Of course there are differences, in a category we might have additional diagrams to express axioms such as associatively, in an interface/trait/typeclass there is no way to enforce axioms.
Also, in a computer program, functions don't always have the same properties a mathematical functions. A mathematical function should always produce the same output for a given set of inputs. In a program a function will often depend on an input, or a state value, or something like that. In the programming world the first case is known as a 'pure function' and the other cases are known as 'side effects' or just 'effects'.
Computer Languages and Algebras
Computer languages incorporate algebras and algebra-like structures into the language, for instance they have fundamental types such as Integers and float which approximate the corresponding algebras. The users can then build up more complex algebras such as complex, vectors and so on (or use pre-build mathematical libraries).
However, in a mathematical program, it would be good to be able to work with algebras as first class entities in their own right. That is, instead of only being able to construct new algebras by recompiling, we would want to construct algebras dynamically from within the program(this may be related to the idea of category as a first class object?). What we want to do is be able to manipulate these algebras to say, generate its dual or generate the product, sum or exponent of two algebras, or to work with whole families of algebras.
Most languages allow us to construct instances of an algebra, for example '1' as an instance of Integer and then combine them together using functions and operations like '+' however there is no obvious way to treat the whole algebra as a whole entity.
Constructs like 'lists' represent functors, that is it is not a category itself but it maps from a category 'Integer' to a category 'List Integer'.
| List | ||
| Integer | -> |
List Integer |
| This comes close to the idea of dealing with a whole algebra, for instance we can work with elements of the list such as 'a', 'b' and 'c' and we can work with the whole list as a single entity: | myAlgebra:Set A := ['a','b','c']. | ||||||
| So what would it take to turn this into an algebra? Many algebras are built on the concept of set rather than list so we can use 'set' as the functor: |
|
||||||
| Then we need to add structure to the set in the form of functions with signatures like: | mult: (a:myAlgebra, b:myAlgebra):myAlgebra |
Algebra Types
Ω-Algebra
A set of operator symbols, each operator has an arity and all operators act only on the elements of the algebra.
F-Algebra and F-Coalgebra
F-Algebras and F-Coalgebras are the same as Ω-(co)algebras except we denote all the operator signatures by a single functor.
If I may misuse notation then I will notate this as:
Poly := () } n0 times
/\ (%) } n1 times
/\ (%,%) } n2 times
/\ (%,%,%) } n3 times
...
So we can use this to define a free, pure algebra and a pure coalgebra as follows:
UniversalAlgebra() : Metacategory == with
Poly % -> %
UniversalCoalgebra() : Metacategory == with
% -> Poly %
These represent free algebras and a particular instance can be formed by choosing values for the 'components': n0,n1,n2...
F-algebras and F-coalgebras are themselves categories. They can also be defined over an arbitrary category % where Poly % -> % is an endofunctor from % to itself.
On their own pure algebra or coalgebra would not be much use, they don't have a way to interact with other algebras, but perhaps we could add that later.
Monads and T-Algebras
A T-Algebra is an F-Algebra, as defined above, together with a set of equations (axioms) built from the F-Algebra operations.
So we have the endofunctor but what are the two natural transformations to construct a monad from it?
Let T be a (finitary) equational theory, consisting of finitely many operational symbols, each of some arity and a set of equations between terms built from these operations.
Algebra and Coalgebra
If we look at an equation like a+b=c we can interpret this in either a static or dynamic way:
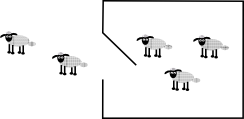 |
Dynamic (coalgebra)We could look at an equation like 2+3=5 as meaning that we start with say, 3 sheep then we add 2 more to get 5. |
 |
Static (algebra)Or we could look at 2+3=5 statically (not changing over time) for instance, if there are 2 sheep in one field and 3 sheep in another field, then that is equal to 5 sheep in another field. |
Algebras tend to be associated with the static situation and coalgebras with dynamic systems.
| Coalgebra | Algebra | |
|---|---|---|
| dynamic behavior oriented systems | static data oriented systems | |
| information | semantics | syntax |
| language type | object oriented | functional |
Algebra
Here is an example of a simple calculator that implements a pure algebra (well almost, I've had to compromise a bit). The idea is that the two operands are on the left and the result of adding, subtracting and multiplying them are shown separately on the right. So the whole thing should be stateless, that is the result only depends on the current input, not some particular sequence. I compromised a bit on this in that I did not want to keep checking if the inputs have changed so I added buttons to trigger calculation of +, - and *.
Coalgebra
This is more like a conventional calculator which is a state machine, that is the inputs act on the state machine.
This state machine is similar to an object in object oriented programming. So when we want to add something to it, we pass the quantity to be added, and its state changes to reflect that, its original state is lost. In this case there are additional states associated with the memory and back functions.
Concepts
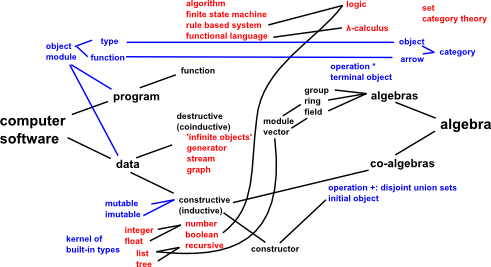
Here are some of the concepts involved and a non-rigorous indication about where there may be links.