Maths - Category Theory - Compound Categories

Here we look at building new categories from existing categories:

• Opposite Category
• Sub Objects
• Product (categorical product)
  • Pullback
• Sum/Co-product
• Initial Object
• Exponent.
• Cartesian Product.
• Tensor Product.
• Functor Category.
• Comma/Slice Categories.
• Quotient Categories.

Opposite

There is a duality between categories by reversing the direction of the arrows.

The opposite category of C is denoted C^op

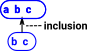
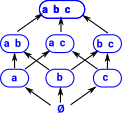
Sub Objects

This is a generalisation of subset.

The concept of a sub-object is related to these concepts:

• Equivalence as described on page here.
• Subobject Classifier on page here.
• See page here for a non-categorical approach to sub-objects.

Catagorical Limits

Generalises universal constructions such as:

• products
• pullbacks
• inverse limits

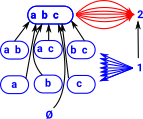
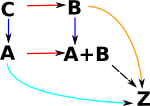
In some category C we have: A diagram, defined below, for now we can think of as a 'shape' containing objects and morphisms of C. An object which has morphisms to all the objects in the diagram. Everything constructed like this is supposed to commute. This is called a cone.

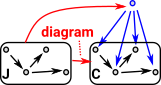
There may be other objects that have morphisms to all the objects in the diagram. The limit chooses the 'best' one.

In this case the 'best' one is the cone which all the others factor through.

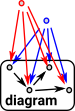
To make this more rigorous and categorical we need to define the diagram better. A diagram of shape J in C is a functor from J to C

More about limits on page here.

Product and Sum

There are some 'universal constructions' such as product, sum and exponent that are objects that appear in many categories.

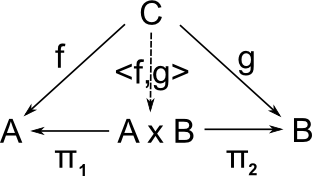
	Product (pullback) More on this page	Sum (Coproduct) (pushout) More on this page
universal cone over diagram
generalisation	a kind of limit	a kind of colimit
set example	cartesian product {a,b,c}*{x,y}= {{a,x},{b,x},{c,x},{a,y},{b,y},{c,y}}	disjoint union {a,b,c}+{x,y}= {a,b,c,x,y}
group	the product is given by the cartesian product with multiplication defined componentwise.	free product the free product for groups is generated by the set of all letters from a similar "almost disjoint" union where no two elements from different sets are allowed to commute.
Grp (abelian)	direct sum	direct sum consists of the elements of the direct product which have only finitely many nonzero terms (this therefore coincides exactly with the direct product, in the case of finitely many factors) the group generated by the "almost" disjoint union (disjoint union of all nonzero elements, together with a common zero)
vector space	direct sum	direct sum
poset	greatest lower bound meet	least upper bound join
base topological space		wedge
POS	greatest lower bounds (meets)	least upper bounds (joins)
Rng
Top	the space whose underlying set is the cartesian product and which carries the product topology	disjoint unions with their disjoint union topologies
Grf
category	objects: (a,b) morphism: (a,b)->(a',b')

tensor products are not categorical products.

In the category of pointed spaces, fundamental in homotopy theory, the coproduct is the wedge sum (which amounts to joining a collection of spaces with base points at a common base point).

Sum

When generating a sum for objects with structure then the structure associated with the link can be added to the sum object.

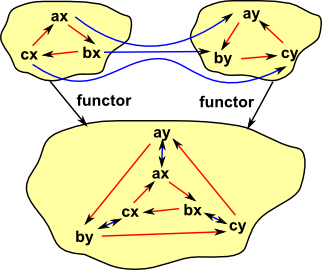
Product

Products for groups are discussed on this page.

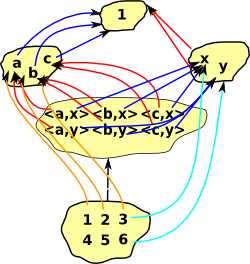
Cartesian Product

Here we extend the idea of a cartesian product of sets to other categories. The categorical product concept above defines the product by its external relationships which is the most categorical way to do it. Here we take a slightly less categorical approach and use the objects and arrows of the categories being multiplied to define their product. We treat the categories as set + structure.

The objects of the product are the same as the cartesian product of sets.

The arrows are combined in a similar way to the Cartesian and tensor products of graphs.

We can extend the concept of cartesian product of sets to categories as follows:

Here is an ordinary cartesian product of sets.
Here we have sets with structure, represented by arrows. An arrow (a, b) -> (a', b') exists in A×B if and only if either: a = a' and b->b' exists in A, or b = b' and a->a' exists in B.

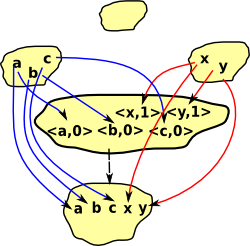
Tensor Product

More about this on this page.

We can extend the concept of cartesian product of sets to categories as follows:

The objects are the same as cartesian product of sets but the arrows are different from the cartesian example above. There is an arrow in AB only if there is an arrow in both A and B. An arrow (a, b) -> (a', b') exists in AB if and only if: b->b' exists. and a->a' exists.
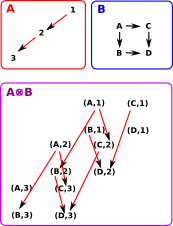Looking at the case above it looks like we could recover projections to A and B from AB. However, is there an example where we can't, where one of the operands has a object with no arrows leaving it? On the right is a diagram of an extreme case where one of the operands has no arrows. In this case, by the definition given above, the tensor product will have no arrows. In this case there may be a projection from A0 to 0 (that would be the Cartesian set product) Would there be an arrow from A0 to A? maybe so, if we take a graph with no arrows as being an initial object. Perhaps this is an example which shows the cartesian product of graphs is not a product in the category theory sense?
A graph with a single object and an arrow to itself is the unit: 1.

Exponential

This is a universal structure but not a limit.

more here.

Functor Category.

We can construct a new category from an existing category 'C', where:

• The objects are the functors of 'C'.
• The morphisms are the natural transformations of 'C'.

More about Functor Category on page here.

Example of Functor Category

The category of all directed graphs is the functor category Set^C. (see presheaves on page here)

Where C is a category with two objects connected by two morphisms

see Yoneda embedding.

Comma/Slice Categories.

More about Comma/Slice categories on this page.

Quotient Categories.

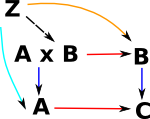
Imagine two categories C and G. Construct a category C/G Its objects are the objects of C that have arrows to G. Its morphisms are the functions which make the diagram commute.
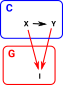This can partition the morphisms.

 

EuclideanSpace

home

Books

Conceptual Mathematics - This is a book about category theory that does not assume an extensive knowledge over a wide area of mathematics. The style of the book is a bit quirky though.

Set Symbols

Group Theory

Functional Programming and Category Theory

Category Theory