Maths - Category Theory - Yoneda

Introduction

I tend to think of category theory as a way to define things from the outside (that is the fuctions/functors going in or out of it) in contrast set theory could be thought of a building up structures from inside. Yoneda gives us a way to link these two viewpoints.

So in category theory: we understand an object by its action on all other objects (or by the action of all other objects on it).

This leads us to the concept of 'representable functors' which gives us all the functors going into or out of an object.

Yonada

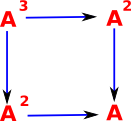
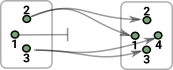
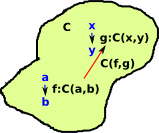
So in some category C. To characterise an object a of C we take all the morphisms out of it. The morphisms are potentially hom-sets to every other element. See page here for more discussion of homsets in a category theoretical context. On the diagram I have added two additional objects x and y. The homsets to these objects are labeled X and Y.
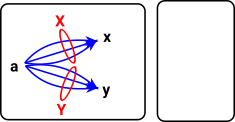These homsets X and Y can be interpreted as sets and so we can show them in a category of sets. Any structure in C, indicated here as a morphism f, is then reflected as a morphism F in set. This can be shown by composing the arrows in the diagram. That is, if we assume 'f' is fixed and we know a->x then we can compose them to get a->y. So the category C can be represented in set.

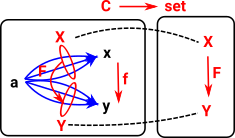This does not apply in every category. It requires that the above morphisms exist and the diagrams commute properly. If all these conditions are met then the category is called representable.

Now we change to look at all the morphisms into an object x. The mappings out of f are contravarient. That is, if we assume 'f' is fixed and we know b->x then we can compose them to get a->x.

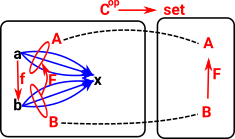And we can look at both. It may be clearer to look at this in the graph category as described on page here.

Yoneda Embedding

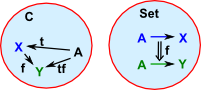
Yoneda allows us to relate categories to sets.

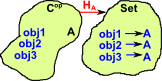
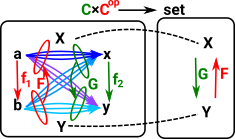
From above we have: C×C^op->set.

Uncurrying gives: C->set^Cop.

That is a map from C to set

Category Theory	Set Theory
Category theory models mathematics by arrows (morphisms/functors) between objects. Higher order structures are given by arrows between arrows (natural transformations) and so on.	Set theory models mathematics by the relationship between sets and their elements. Higher order structures are given by sets within sets and so on.

The Yoneda embedding is an arrow between these.

Generalising

We want to map morphisms to elements of a set. We can start with a mapping 'Q' which maps morphisms in a category 'C' to morphisms in Set.

We choose an object of C called 'A' and an element of Q(A) which we call 'q'.

So that, for all B:

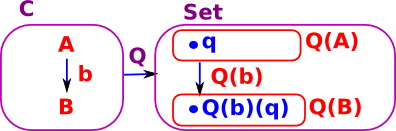
We can then use Q(b)(q) to link q to b.

we have an isomorphism of sets:	C(A,B) -> Q(B)		C(A,-)Q
which maps elements:	b:A->B |-> Q(b)(q)

or equivalently an isomorphism of functors.

The functor Q:C -> Set is called representable.

Covarient and Contravarient Functors

There are two ways that a given morphism can preserve structure:

This is the covarient case where the start of the arrow in C maps to the start of the arrow in D and the end of the arrow in C maps to the end of the arrow in D.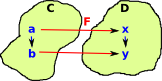
This is the contravarient case where the start of the arrow in C maps to the end of the arrow in D and the end of the arrow in C maps to the start of the arrow in D.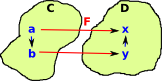

	Unless otherwise stated we usually assume that a morphism/functor is covarient so we can draw this as on the left.
	For the contravarient case we could invent some sort of special symbol for a contravarient morphism/functor. However is usually easier to reverse the internal arrows in either C or D. On the left we have reversed C by making it Cop. So now we can use an ordinary arrow between C and D.

The way that covarient and contravarient functors arise, in this case, is as follows.

Let 'A', 'X' and 'Y' be elements of a class 'C'. let 'f' be a functor from 'X' to 'Y'. Assume that both 'A' and 'f' are fixed:

covarient	contravarient
If 'f' and 'h' are known then we can derive 'g' (by composition) If 'f' and 'g' are known then we cannot derive 'h' (see concepts of section and retraction). So given some fixed 'f' the 'g' depends on 'h' which I have drawn below as an arrow between arrows.	If 'f' and 'g' are known then we can derive 'h' (by composition) If 'f' and 'h' are known then we cannot derive 'g' (see concepts of section and retraction). So given some fixed 'f' the 'h' depends on 'g' which I have drawn below as an arrow between arrows.
This arrow goes in the same direction to f, hence it is covarient.	This arrow goes in the opposite direction to f, hence it is contravarient.

We now need to combine these ideas with the concept of hom sets as follows.

Hom Functors

For more information about homsets see the page here.

Given a category with objects such as: a,b...x,y f:C(a,b) represents all the morphisms from a to b. g:C(x,y) represents all the morphisms from x to y. We can now take this up one level. A hom functor C(f,g) represents all the functors from f to g.

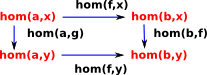We require this hom functor to interact nicely with the hom sets so the diagram on the left needs to commute.

This gives rise to a bi-functor to the category of sets:

C^op×C->Set

A bifunctor is a functor in two arguments, it could be written H(C^op,C)->Set . That is, it is contravarient in the first argument and covarient in the second).

Representable Functors

(There are some good diagrams on ncatlab)

Given a locally small category C, and an object C, the functor: HomC(C,−):C->Sets that sends objects to hom-sets and arrows f:A->B to functions: f*:HomC(C,A)->HomC(C,B) g |-> f•g is (or is isomorphic to) the Representable Functor.

In category theory we tend to work in terms of functors rather than objects, sometimes functors have more useful properties than objects. Representable Functors allow us to convert objects into functors. There are two ways to do this, either to or from a given object A.

	covarient representable at A	contravarient representable at A
	So each element xX maps to a whole function f*:A->X where: X and A are objects in C, we think of A as being fixed.	So each element xX maps to a whole function f*:X->A. That is: 'f*' doesn't just map x to an element of A but it maps every element of X to A. where: X and A are objects in C (or Cop so that we don't have to denote a covarient functor), we think of A as being fixed.
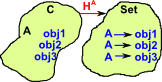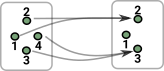
diagram		We think of X as being variable, here shown as obj1, obj2, obj3... f a is isomorphic to x -> a.

Example - An example of representable functors is powerset as described on this page.

Representable in Graph

A representable in graph is an object with two vertices and an edge between them. See page here for a fuller description of this.

Representable in Group

In a group there is only one object so the representable object is the same. This is a fixed size set and the morphisms are permutations to itself. More about group on page here.

Covarient and Contravarient in Representable Functors

Here we combine the covarient and contravarient discussion above with representable functors to explain why representable functors come in covarient and contravarient types.

So far in representables we have mapped a element of an object to an element of a homset, but we want to know if this map preseves structure, so here we will see what happens when we map a whole function 'f':

covarient	contravarient
From the triangle on the right of the diagram we have: hom(A,Y) = f • hom(A,X) that is post compose with f So f maps to: hom(A,X) -> hom(A,Y) which is: hom(A,X) -> f • hom(A,X)	From the triangle on the right of the diagram we have: hom(A,X) = hom(A,Y) • f that is pre compose with f So f maps to: hom(A,X) -> hom(A,Y) which is: hom(A,Y) • f -> hom(A,Y)

Example 1 - Groups

This is Cayleys theorom. A group is a simplified case because there is only one object. If we consider a group as a set with permutations (reversable functions) then there is only one object: G. So HomC(C,−) becomes G -> HomC(G,G). The Hom set is therefore the set of all the actions of the group which correspond to the elements of the group. So this is just the forgetful functor from the group to its underlying set.

Here we want to relate permutations to other definitions of groups.

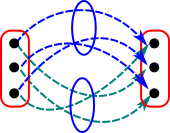
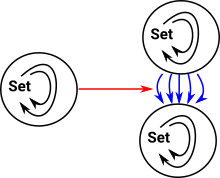
So here we have a simple group, for example, in this case a cyclic group shown as a Cayley diagram:

Here we are looking at functors between the structures which preserve structure.
Here we apply one element of the group, in this case '2', as a representable. This must 'play well' with the internal structure of the group.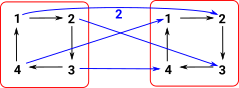
If we repeat this for all permutations we get a set of permutations (homset).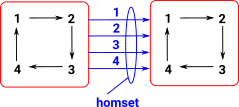

Cayley's theorem is more full dicussed on this page.

Example 2 - Relating Homology and Cohomology

See the page here.

Example 3 - Transforms in 3D Space using Quaternions

See the page here.

Further Notation

Given any object AC there are two types of representable functors:

HA = C(-,A) =Cop(A,-)	is a contravarient representable at A
HA =C(A,-)	is a covarient representable at A

as follows:

	contravarient representable at A	covarient representable at A
type:	HA: Cop -> Set this is a presheaf	HA: C -> Set
objects:	X C(X,A)	X C(A,X)

where:

• C(,) is a hom-set of functors in C.

We are generating as set of functors to/from the object 'A'. The object 'A' is related to the concept of initial (covarient case) and terminal (contravarient case) objects.

A functor H: C -> Set is representable if:

• C and Set are small
• H preseves all small limits
• There exists a small set 'Set' of objects of C such that for any object cC and any element xH c there exists an sSet, an element yH s and an arrow f:s -> c with (H f)y = x.

So if objects in C map to functors in Set what happens to functors in C? We can represent them as natural transformations:

	contravarient representable at A	covarient representable at A
type:	HA: Cop -> Set	HA: C -> Set
objects:	X C(X,A) HA = C(-,A) =Cop(A,-)	X C(A,X) HA = C(A,-)
diagram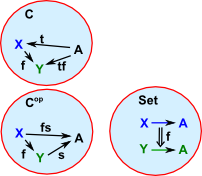
Example in set. So, for this example, we take C to be a set containing 3 elements: a, b and c.	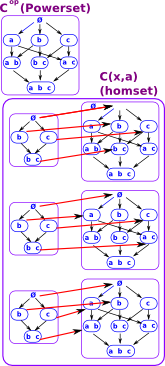Usually when working with natural transformations we can look at components in the codomain but, in the contravarient case, this is not very useful because everything maps to 'A'. So in this case C is like a component in the domain.

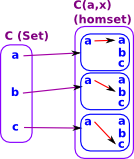Other examples:

• Group -> Cayley's theorem
• posets -> Upper sets

Square Bracket Notation

[A,B] takes two categories A & B and produces a new category as follows:

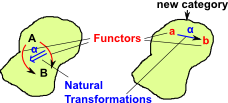The functors from A to B become the objects. The natural transformations become the arrows.

Yoneda

So far given any AC we have:
A H_A[C^op,Set]
this extends to a functor:
C [C^op,Set]

The arrows in the category are distinguished by their effect on generaised elements based at A. Such an object A is called a generator for C.

Looking at objects of C [C^op,Set] we have:

A		HA
.| f \/		Hf natural transformation
B		HAHB

component of H_f at XC

(H_f)_X: H_AH_B

	f _
C(X,A)		C(X,B)

The Yoneda lemma, in any locally small category C then,

[C^op,Set](H_A,X)X(A)

naturally in AC and X[C^op,Set]

Both the left and right sides are sets of natural transformations. [C^op,Set](H_A,X) is the set of natural transformations in [C^op,Set] from H_A to X.

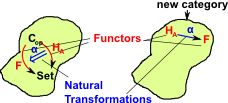where: C is a category [Cop,Set] - Here we apply the above construction to Cop and Set. Cop is the dual of C, that is, all the arrows are reversed. For any object A of C there is a functor: HA: Cop -> Set (also written C(-,A)) this functor is defined on objects HA(B) = C(B,A) and on morphisms by HA(f) = f* (compose with f) X is a functor Cop -> Set For any category D and objects D,D' of D the set of morphisms from D to D' is written D(D,D')

Example 1 - Groups

When we represent a group as a permutation group each permutation (arrow) can be mapped onto a set element.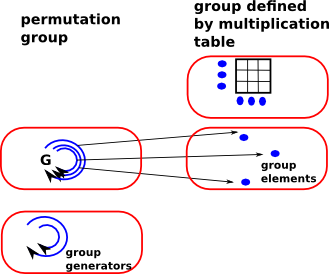

The composition of the arrows with their associatively and identity then naturally map onto the group multiplication with its associatively and identity element.

Example 2 - Sets

We have two sets, 'A' and 'B', with an arbitrary mapping 'F' between them. We can define a subset of set 'B' by using the predicate 'P'. For every subset of 'B' defined by 'P' there exists a subset of 'A' defined by 'R'.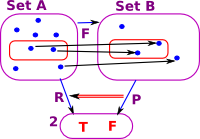
However this does not necessarily work in the other direction. Here is an example of a subset of 'A' which does not map to a subset of 'B'.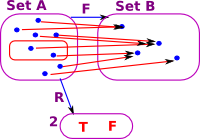

So the map 'F' between objects induces a contravarient map between arrows P->R.

For more information about this relationship between sets and boolean logic see the page about topos theory.

Program

Can we do somthing similar to the Yoneda embedding to a object oriented program? Here is a simple example written in 'Scala':

class Complex(r: double, i: double) {
  val real = r
  val imag = i

  def +(that: Complex) = new Complex(real + that.real, imag + that.imag)
  def *(that: Complex) = new Complex(real*that.real - imag*that.imag,imag*that.real+real*that.imag)
}

It has two values: real and imag (that I take to be like objects) and two operations: + and * (that I take to be like functors).

Presheaf

A V-valued presheaf F on a category C is a functor F:C^op -> V

In the theory of topological space a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space.

More about presheaf in category theory on page here.

Yoneda Proof

On site here is a proof written in Isabella.

EuclideanSpace

home

Related Pages

• Yonada involves the Hom set which is discussed on page here.
• Also exponential object.
• Hom sets are used in the page about the Yonada Lemma to relate structures at different levels of abstraction.
• The page here discuses homsets from a set theory perspective.
• Other related pages are:
  • functors
  • arrows
  • Functor Category
  • Presheaves
  • internal hom-set

Functional Programming and Category Theory

Representation Theory for Simplicial Sets

see wiki.

The Yoneda Embedding (see page here)

Assume a category C where the objects are sets of points and the morphisms are total functions.

allows us to represent categories in set.

The opposite category to this Cop has the same objects but the morphisms are opposite which means elements in the domain may map to zero or multiple elements in the codomain. This corresponds to face maps and degeneracy maps in simplicial sets.

Adding an additional point (origin) allows each point to be represented as a vector. Then the morphism is represented by a matrix.

More about representation theory for simplicial sets on page here.

Euclidean Space