n-Categories
This is often described in terms of n-cells. In the diagrams below, the number of lines (shafts) in the arrows indicates the order of the arrow.
| 0-cell | 1-cell | 2-cell | 3-cell |
|---|---|---|---|
| object | arrow | arrow between arrows | arrow between arrows between arrows |
 |
 |
 |
 |
More about n-categories on this page.
2-categories
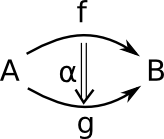
A 2-category C has:
- A class of objects.
- For a pair of objects a category (not set) hom(x,y).
- Objects of hom(x,y) are morphisms of C.
- Morphisms of hom(x,y) are 2-morphisms of C.
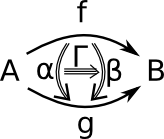
Composition is:
hom(x,y) × hom(y,z) = hom(x,z)
Weak vs. Strong
If associativity and unit laws are upto equality then 2-category known as strong
If associativity and unit laws are upto isomorphism then 2-category known as weak
- weak 2-category known as bicategory.
- strong 2-category known as 2-category.
n-categories with only one object
from Categorification John C. Baez, James Dolan:
| k | n=0 | n=1 | n=2 |
| 0 | sets | categories | 2-categories |
| 1 | monoids | monoidal categories | monoidal 2-categories |
| 2 | commutative monoids | braided monoidal categories | braided monoidal 2-categories |
| 3 | " | symmetric monoidal categories | weakly involutory monoidal 2-categories |
| 4 | " | " | strongly involutory monoidal 2-categories |
| 5 | " | " | " |
Quasi-Category
A quasi-category is a generalisation of the notion of a category. In a category the composition of two morphisms is uniquely defined but in a quasi-category all the morphisms that can serve as composition of two given morphisms are related to each other by higher order invertible morphisms.
Definition of Quasi-Category as a Simplicial SetA quasi-category is a simplicial set A in which every inner horn can be extended (not necessarily uniquely) to a simplex. That is, for every map /\k[n] -> A (0<k<n), there exists an extension Δ[n] -> A along the inclusion /\k[n] ->Δ[n]. |
 |
Where:
|
Example of a 2-dimensional simplex. |
Example of a 2-dimensional horn with face opposite 0 missing. |
More about:
