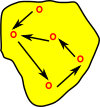
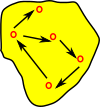
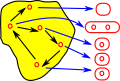
There are different ways to define a groupoid such as:
- Algebraic definition: same definition as a group but with a partial function replacing the binary operation.
- Categorical definition: a category in which every morphism is invertible.
- As an oriented graph where every edge has an inverse.
As discussed on the page here groupoids can be thought of as a weakening of a setiod. Instead of equivalences we have isomorphisms, that is the permutations show how objects are equal in multiple ways. |
 |
Applications
Groupoids form the underlying structure in homotopy type-theory (HoTT) Discussed on the page here.
n-Groupoids
| Level | In Type Theory | Represents Equality in Hott see page here |
|
|---|---|---|---|
| -2-Groupoid | contractible singleton (Unit Type) |
||
| -1-Groupoid | subsingleton (Mere proposition) |
||
| 0-Groupoid (n-lab) | Set | Example - equality in Natural Numbers | |
| 1-Groupoid (n-lab) | Example - equality in Monoid | ||
| 2-Groupoid (n-lab) | Example - equality in Category |
Groupoids and Equivalences
| Group Definition | Equivalence Definition | |
|---|---|---|
| Identity | a = a•Id = Id •a | reflexivea~a |
| Reverse | a•inv(a) = inv(a)•a = Id | symmetricif a~b then b~a |
| Associatively | a•(b•c) = (a•b)•c | transitiveif a~b and b~c then a~c |
A groupoid is a setoid with natural coherence axioms. A setoid is a set with an equivalence relation.
Another special case is G-sets, sets with an action of a group G.
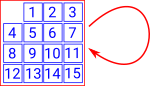
Example 1 - Fifteen Puzzle
There used to be a puzzle, sometimes called the 15 puzzle, consisting of 15 sliding plastic tiles in a 4 by 4 frame. There is only one space without a tile, so the only moves possible are to slide the adjacent tiles into that space. The tiles have letters or numbers on them and the goal is to get them in a certain order. |
 |
For more discussion about this example see page here.
This example illustrates the different ways of defining the groupoid:
|
 |
|
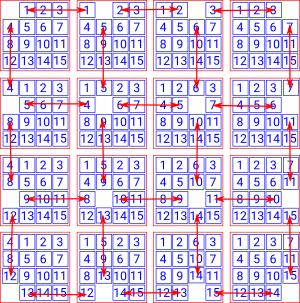 |
So we could specify the state of the game by:
- The starting position.
- Together with the sequence of positions of the holes.
Since all arrows are reversible we can always get back to a previous state by retracing a path back. However, if we start with a hole in a particular place and then follow a circular path (for the hole) so the hole ends up in the same place the state (position of tiles) may change so this is not equal to Id.
Example 2 - Isomorphic Sets
Imagine if we have multiple sets, all of the same size, then they can all be 'equal' in multiple ways. That is we may have:
and so on for the other sets of the same size. This gives a groupoid like structure. |
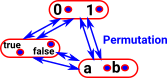 |
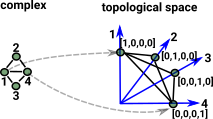
Example 3 - Topology / Homotopy
Fundamental Groupoid
Example 4 - Can Simplicial Sets be modeled by Groupoids?
Does this diagram show a groupoid? No, because the mappings are not all reversible. We can reverse a degeneracy map with a face map but the face map is not reversed by the degeneracy map unless it is already degenerate. |
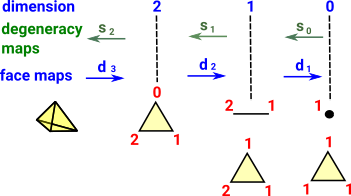 |
What if we take the more complicated situation where multiple faces are glued together. Is there some way we can characterise this as a groupoid? It feels like the fifteen puzzle above in that jumping between vertices, edges, triangles, etc. allows us to get to different faces. |
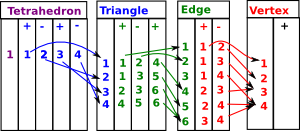 |
To get this to work as a groupoid I think we need some more concepts:
The nerve functor N : Grpd -> sSet embeds Grpd as a full subcategory of the category of simplicial sets. The nerve of a groupoid is always a Kan complex. (see wiki)
Computational Path
Here we are looking at the relationship between two types of equality: definitionally equality and propositional equality. These are explained on this page.
In Nat consider 'n', '0+n' and 'n+0' they are equal terms in some way. 'n' and '0+n' are definitionally equal because they automatically normalise to the same. Definitionally equality is denoted with a 3-bar equals sign (≡) or just by using the same symbol. But 'N+0' is propositionally (but not definitionally) equal to N. It is denoted with a normal equals sign (=) and shown as an arrow between nodes. |
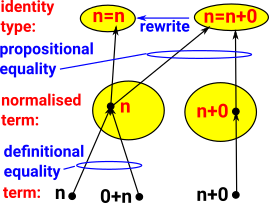 |
This can get more complicated when we have types involving containers within containers. |
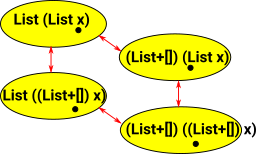 |
Example 5 - Groupoids and Type Theory
| Type Theory | Groupoids |
|---|---|
a,b : A |
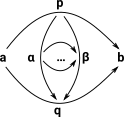 |
More about type theory on page here.
Categorical Definition
| Categorical Definition | Groupoid Definition | |
|---|---|---|
| Identity | Arrow from all objects to themselves that do not change it. | Identity element exists |
| Reverse | Arrows not generally reversible. | All arrows can be reversed. f • f-1 = Id |
| Associatively | Composition of morphisms | Associatively |
A groupoid is a category in which every morphism is invertible. So this means that, when objects are connected by arrows, they are Isomorphic. However, just because the objects are isomorphic, does not mean the structure is not complicated as we saw with the 15-puzzle.
If the category is based on an underlying set then we can think of the arrows as permutations.
 |
In an ordinary group (represented a permutation group) the functors are endofunctors with only a single object. |
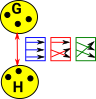 |
In a groupoid the permutations can go between objects. Because the mappings are reversible the objects are isomorphic, we can get back to Id, however we don't have to use the reverse so its possible to use the round trip to permute the elements. |
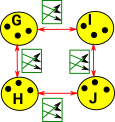 |
Its possible to have permutations such that we can only permute the elements if we go round the loop but not if we reverse the path. Depending on the complexity of the groupoid there may be multiple paths round the loop which produce the same permutation so we have possible equivalences between paths. That is, higher order equivalences. |
ω-groupoid
An ω-groupoid is an ω-category in which all higher morphisms are equivalences.
A ω-category (or ∞-category) is a higher order category.
- all composition operations are strictly associative.
- all composition operations strictly commute with all others (strict exchange laws).
- all identity higher morphisms are strict identities under all compositions.
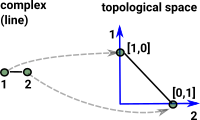
Fundamental Groupoid - Topology
The fundamental groupoid of a space is a groupoid with:
- Objects - points of a space.
- Morphisms - paths in X, identified up to endpoint-preserving homotopy.
| ω-groupoid | topological space | |
|---|---|---|
| type | space | |
| term | point | |
| path(x,y) | Id(x,y) paths from x to y in the space. |
Also see fundamental groupoid on page here.
Groupoid in Type Theory
- Used in Homotopy Type Theory (HoTT) see page here.
Computer Model of Groupoid
A model of a groupoid might contain a hierarchy of types:
- base : Type
- path : base -> base
- path2 : path -> path
- path3 : path2 -> path2
So the easiest base type to think about might be, for instance, a finite set. In that case a path would be the possible equalities between the elements of the set. This is a reversible mapping which is a permutation.
What would path2 look like? That is a mapping between permutations.
In the 15-puzzle example there is only one mapping (path) at most, between any two nodes. So the higher path is just a trivial Id mapping, then its trivial mappings all the way up. So that doesn't give us any intuition about higher level paths. Perhaps if we added some ability to switch routes (like a railway switching game?) would that do it?
Oidification
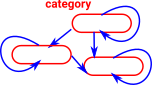
Oidification allows us to start with a single object and one (or more) arrows back to itself and generalise this to multiple objects. This new structure does not need to have arrows between every pair of objects but composition always exists and every object has an identity arrow.
Here the words 'object' and 'arrow' are used in the category theory sense as described on the page here.
Here are some examples:
| Single Object | Multiple Objects | |
|---|---|---|
|
This imposes an external equivalence relation and internalises it. |
An example would be a set with a set with a fixed number of elements. |
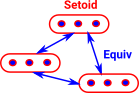 Since the arrows are reflexive, symmetric and transitive this gives an equivalence relation. |
|
This can be thought of as a weakening of a setiod. Instead of equivalences we have isomorphisms, that is the permutations show how objects are equal in multiple ways. |
 |
|
|
Just to confuse things the naming conventions have changed here. Monoid has an 'oid' but this is the single object case. A Monoidoid is a category. |
 |
 |
Implement in Idris
Is it possible to implement a groupoid using Idris?
I was thinking about something like this:
||| Groupoid where base type is a
||| finite set (implemented as a list)
record Groupoid (level : Nat) where
constructor MkGroupoid
source : Nat
dest : Nat
Path : List (Groupoid (level + 1))
fifteenPuzzle : Groupoid 0
fifteenPuzzle =
let
c1:Groupoid 2 = MkGroupoid 1 2 []
c2:Groupoid 2 = MkGroupoid 2 1 []
swap = [c1,c2]
b1_2:Groupoid 1 =MkGroupoid 1 2 swap
b1_5:Groupoid 1 =MkGroupoid 1 5 swap
b2_3:Groupoid 1 =MkGroupoid 2 3 swap
b2_6:Groupoid 1 =MkGroupoid 2 6 swap
b3_4:Groupoid 1 =MkGroupoid 3 4 swap
b3_7:Groupoid 1 =MkGroupoid 3 7 swap
b4_8:Groupoid 1 =MkGroupoid 4 8 swap
b5_6:Groupoid 1 =MkGroupoid 5 6 swap
b5_9:Groupoid 1 =MkGroupoid 5 9 swap
b6_7:Groupoid 1 =MkGroupoid 6 7 swap
b6_10:Groupoid 1 =MkGroupoid 6 10 swap
b7_8:Groupoid 1 =MkGroupoid 7 8 swap
b7_11:Groupoid 1 =MkGroupoid 7 11 swap
b8_12:Groupoid 1 =MkGroupoid 8 12 swap
b9_10:Groupoid 1 =MkGroupoid 9 10 swap
b9_13:Groupoid 1 =MkGroupoid 9 13 swap
b10_11:Groupoid 1 =MkGroupoid 10 11 swap
b10_14:Groupoid 1 =MkGroupoid 10 14 swap
b11_12:Groupoid 1 =MkGroupoid 11 12 swap
b11_15:Groupoid 1 =MkGroupoid 11 15 swap
b12_16:Groupoid 1 =MkGroupoid 12 16 swap
b13_14:Groupoid 1 =MkGroupoid 13 14 swap
b14_15:Groupoid 1 =MkGroupoid 14 15 swap
b15_16:Groupoid 1 =MkGroupoid 15 16 swap
in
the (Groupoid 0) (MkGroupoid 0 0 [b1_2,b1_5,b2_3,b2_6,b3_4,b3_7,b4_8,
b5_6,b5_9,b6_7,b6_10,b7_8,b7_11,b8_12,
b9_10,b9_13,b10_11,b10_14,b11_12,b11_15,b12_16,
b13_14,b14_15,b15_16]) |