Maths - Equality of Terms and Types

On these pages we look equality between terms in a given type. In the context of M-L dependant type theory the distinction between types and terms blurs so we can look at the following as special cases:

• Equality between types.
• Equality between functions.
• Equality between properties (higher order equality).

Equality Of Types

Equality can be defined in different ways, in some cases we need things to be considered equal only when they are defined in exactly the same way, in other cases we need a looser form of equality where things may be defined differently but behave the same in some way.

Definitional Equality

More exact equality happens when the terms are both defined in exactly the same way. The name 'definitional equality' usually allows the terms to be 'normalised' before comparing them. This means that any functions can be applied to expressions, if this reduces them.

Exactly how this normalisation is done may vary. See page here for more details.

Propositional and Leibniz Equality

Propositional equality considers terms to be equal both when they are definitionaly equal and also when they can be proved to be equal. More information about the nature of these proofs and other details of propositional equality see page here.

Leibniz equality considers terms to be equal when they have the same properties. See page here for more details. Propositional and Leibniz equality amount to the same thing.

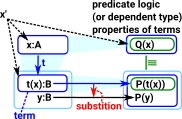
In this diagram P(x) is all properties of x. Every property that is true for x must be true for y.

This is a useful level of equality for computer languages because types that are propositional equal can be treated the same even though they are not defined identically.

Equality in Computer Code

In 'functional' languages like Haskel and Idris information is held in the form given by its constructors. So, if two types have all identical constructors then they are definitionally equal (internal equality). The eliminators are defined in terms of their properties. So if two types have the same eliminator, for all properties, then they are propositionaly equal (external equality).

Identity or Equality Type

In M-L type theory propositional/Leibniz Equality is represented by a type known as an identity type. This type represents a proposition which is true if inhabited (if it can be constructed).

As with other types 'identity types' are defined by their formation, introduction and elimination rules (see table below). It can be hard to get an intuitive understanding of these rules so the remainder of this page attempts to explain them.

type formation Id exists for every pair of terms in A	A:Type Γ, x:A, y:AIdA(x,y) : Type
term introduction reflexivity Id is only inhabited if both elements of the pair are the same.	ΓA:Type Γ , a:Arefl(a) : IdA(a,a)
term eliminator	from ncatlab: Γ,x:A,y:A, p:IdA(x,y)C(x,y,p):Type   Γ,x:A,C(x,x,r(x)):Type Γ,x:A,y:A,p:IdA(x,y)J(t; x,y,p):C(x,y,p)

So lets look at each of these in more detail: (More detail also on this page)

Id Type Formation

We can form any syntactically correct equality as a type, this is called a proposition. These propositions do not have to be true. To 'prove' they are true we construct an instance of them (see term introduction below).

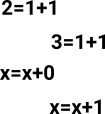Id Term Introduction

Propositions have a single constructor called Refl. We can only construct an equality term if it is true. So any proposition can be formed but only true propositions can be constructed.

Id Term Eliminator

The eliminator tells us how to use a type and it can also tell us what a type 'means'.

In programming a propositional equality between two types allows us to treat the two types interchangeably. Perhaps it is the loosest equality that allows this? How could we express such a conjecture?

To specify the implied types and make things more precise the indentity elimination rule is more fully specified something like this:

Γ,x:A,y:A, p:IdA(x,y)C(x,y,p):Type   Γ,x:A,C(x,x,r(x)):Type Γ,x:A,y:A,p:IdA(x,y)J(t; x,y,p):C(x,y,p)

By Induction

There are other ways to approach the Id term eliminator. We can look at it as an induction idea. We can use proofs to get more equal terms, then apply proofs to these and so on.

Substitution

Substitution of like-for-like only works with exact equality, With something looser, such as isomorphism, we can use transport which allows us to transport properties between types.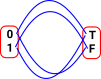

The items on the bottom are equalities and above them are properties. This shows a substitution in the horizontal direction. When the variable changes the property changes appropriately.

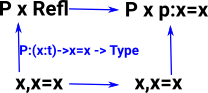Having discussed the background we now get to the definition of the eliminator. The eliminator for equality is known as 'J'. It says:

J : (P : (a,b:t) -> (a=b) -> Type) ->
    ((a:t) -> P a a Refl) ->
    ((a,b:t) -> (p:a=b) -> P a b p)
J P h a a Refl = h a

That is, if a property between 'a' and 'a' is true then the same property between 'a' and 'b' is true if a=b.

If we have two variables represented by the same name then we take this as meaning that they are definitionally equal.

If we have two variables 'a=b' then we take this as meaning that they are propositionaly equal (leibniz equality).

So 'J' is saying that definitional equality has the same external properties as Leibniz equality.

Using 'J' we can prove substitution and the equivalence rules (reflexitivity, symmetry and transitivity).

Substitution as Pullback

Can we express substitution in category theory terms? See discussion on page here.

There is a discussion of this topic on this site.

So why the difference? I think in the predicate case we are going backwards.

Typically a predicate could be an equation which may be true or false depending on the values of its variables. Or a function from a variable to bool (or some truth object).

• More about substitution on this page.
• Using substitution in proofs on this page.

Intuition

As with a lot of powerful mathematical concepts their are multiple ways to understand the equality eliminator:

Oidification

Oidification allows us to start with a single object and one (or more) arrows back to itself and generalise this to multiple objects. This new structure does not need to have arrows between every pair of objects but composition always exists and every object has an identity arrow.

Here the words 'object' and 'arrow' are used in the category theory sense as described on the page here.

Here are some examples:

	Single Object	Multiple Objects
Setoid This imposes an external equivalence relation and internalises it.	The single object needs to have the reflexive relation, that is, be equal to itself. An example would be a set with a set with a fixed number of elements.	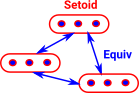Since the arrows are reflexive, symmetric and transitive this gives an equivalence relation.
Groupoid This can be thought of as a weakening of a setiod. Instead of equivalences we have isomorphisms, that is the permutations show how objects are equal in multiple ways.
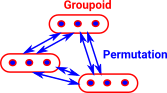Category Just to confuse things the naming conventions have changed here. Monoid has an 'oid' but this is the single object case. A Monoidoid is a category.

Using 'J' Eliminator

Substitution

Refl

Symmetry

Transitivity

Propositional Equality

Propositional equality is effectively the same as Liebniz equality, that is, things are the same if all their properties are the same. Intuitively this makes sense because all the properties can be factored through the constructors/deconstructors.

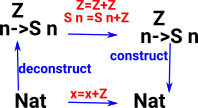Equivalence

There is a more general discussion of equivalence on page here.

Here we are interested in definitions of equivalence that are useful for type theory and especially HoTT.

One definition (see this paper - definition 2.1.2 ): An equivalence AB is a pair (f,e) where f : A -> B and e is a proof that for every b : B the fibre of f at b is contractible.

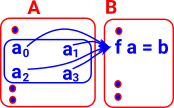
Fiber/Preimage of a Map

We are given an element of the codomain 'b' and a function from A to B called 'f'. From this there must be an element of the domain 'a' with b = f a.

-- The fiber/preimage of a map: fiber (A B : U) (f : A -> B) (b : B) : U = (a : A) * Path B b (f a) (from this site)

For every element 'b' of 'B' this gives us a set of elements of 'A': In order to define equivalence we need this pre-image to be contractible to a single element. So we need to go on to define contractibility.

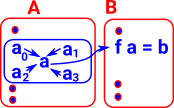
Contractible Type

We are given a type 'A' For this to be contractible there must be a path from an element 'x' to all 'y'. This is saying that type 'A' must have a unique inhabitant

-- contractible type isContr (A : U) : U = (x : A) * ((y : A) -> Path A x y) (from this site)

We can now contract the fibre to give a single element in 'A' to correspond to 'b' in 'B'. So now we have a 1:1 correspondence between 'a' and 'b' so this is looking more like an equivalence.

Equivalence

A map is an equivalence if its fibers are contractible

-- A map is an equivalence if -- its fibers are contractible isEquiv (A B : U) (f : A -> B) : U = (b : B) -> isContr (fiber A B f b) (from this site)

We now have a definition of equivalence in type theory terms. A definition of isomorphism involves finding inverse maps and this does something similar using the pre-image/fibre. However, for this definition of equivalence, we only need to do this in one direction. This is also fairly general in that it is independent of the labels of the elements.

Homotopy Interpretation

If we have two variables 'x' and 'y' they can be considered as two seperate points. These points cannot be compressed into a single point unless x=y.

In HoTT it is possible that x and y can be equal in two different ways so again they cannot be compressed into a single point.

EuclideanSpace

home

This Page

This page is part of a set of pages about type theory, these pages start here.

Related Subjects

On this site:

• For more information about Univalence Axiom see page here.
• For more information about Propositional, First Order and Higher Order Logic see page here.
• More information about setoid and groupoid structures.
• For information about how equality proofs are implemented in the Idris language see this page.
• Equality in category theory.

Other Sites

• http://strictlypositive.org/obseqnow.pdf

Equality

In Set Theory More on page here.		Two sets are equal if they contain the same elements (Principle of Extensionality). If the set has structure then that would also have to be equal in some way.
In Category Theory More on page here.		Often when comparing types we need some loser way of considering that two types are essentially the same. Isomorphism is frequently the most appropriate type of equality. This is defined using a category theory way, that is, by external morphisms.
In Type Theory More on page here.	vec(x)=vec(x+0)	In M-L type theory the Identity type is often used. If things are equal in this way they can be interchanged when used in computer programs.
In Type Theory More on page here.		In Homotopy Type Theory (HoTT) there is a different way to get isomorphism from equality. That is to allow types to be equal in many ways.