Equality Rules

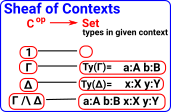
There are rules for both definitionally equality and propositional equality

Rules for Definitionally Equality

The rules must be normalising so,

• All rules must reduce the expression in some way as the rules are applied automatically and there must be no possibility of a loop where rules get applied indefinitely.
• The evaluation of an expression containing only literal values will give a value.
• There may also be rules for expressions containing variables as long as these rules are sure to terminate but these rules may be more ad hoc. For example, in Idris function parameters that are not case-split may be reduced.

As an example, a rule for symmetry x=y -> y=x can't be a definitionally equality rule and so must be a propositional equality rule because:

• It may not be necessary.
• If applied automatically it would be called indefinately.

Rules for Propositional Equality

The rules are used to prove equality so its harder to have some automatic algorithm and so the programmer needs to apply the rules as required to do the proof.

Substitution

There seems to be at least 2 sorts of rules we can apply to equations:

• Change variable to another variable or expression (provided we do it consistently everywhere it occurs, including in types and in context)
• Replace like for like.

If we substitute, in a term M all occurrences of context variable x by a term N of the same type as x, then the result is the same type - it will remain true.

ΓN:σ Γ,x:σ, ΔM Γ,Δ[N/x]M[N/x]

example where: N= y+1 M = a x² + b x + c

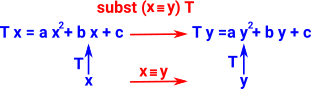
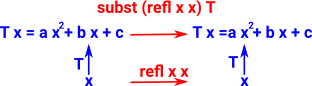
Definition of 'subst'.

subst takes T x to T y.

We can think of T x as being an expression in x. So subst takes an expression in x to an expression in y.

q:(x=y)T : A -> Typet :T x subst q T t : T y

Below is the computational rule where the two values are already definitionaly equal. Here refl (propositional equality) is embedded into this definitionaly equality.

(subst (refl x x) T t)t : T x

Also we can replace like for like in equations (is this substitution?).

Rewriting in Logic

Rewriting an expression into a logically equivalent one.

example: ¬A /\ ¬B -> ¬(A \/ B)

Computation rule Refl disappears when properties are definitionaly equal.

subst (Refl P)P

id:{A: Set}->A->A
_==_:{A: Set}->A->A->Set
 subst:{A: Set} (C:A->Set) {x y:A}->x==y->C x->C y

subst : forall {x y} -> x == y -> x -> y
subst refl x = x

||| Perform substitution in a term according to some equality.
replace : {a:_} -> {x:_} -> {y:_} -> {P : a -> Type} -> x = y -> P x -> P y
replace Refl prf = prf

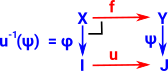
Substitution as a fibration
example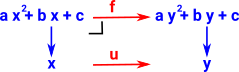

EuclideanSpace

home

Related Subjects

For more information about Univalence Axiom see page here.

For more information about Propositional, First Order and Higher Order Logic see page here.

Idris Let notation explained here.

Contexts in Type Theory

Contexts come from logic and are used in type theory to hold information about variables. C is a category of contexts and the individual contexts are denoted by upper case Greek letters: Γ,Δ… 1 is empty context.
The structure of contexts is a sheaf: Cop -> Set.
Morphisms between sheaves represent substitutions.

More about contexts on page here.

Equality

In Set Theory More on page here.		Two sets are equal if they contain the same elements (Principle of Extensionality). If the set has structure then that would also have to be equal in some way.
In Category Theory More on page here.		Often when comparing types we need some loser way of considering that two types are essentially the same. Isomorphism is frequently the most appropriate type of equality. This is defined using a category theory way, that is, by external morphisms.
In Type Theory More on page here.	vec(x)=vec(x+0)	In M-L type theory the Identity type is often used. If things are equal in this way they can be interchanged when used in computer programs.
In Type Theory More on page here.		In Homotopy Type Theory (HoTT) there is a different way to get isomorphism from equality. That is to allow types to be equal in many ways.