At school I remember learning how to do arithmetic with numbers, then it went on to 'algebra' by introducing equations and variables and so on. So what exactly is the definition of 'algebra' and 'an algebra' such as 'matrix algebra'?
It seems that, for a subject so fundamental to mathematics, its quite hard to find precise, simple and consistent definitions.
What Is Algebra?
As I say, for something so fundamental its surprisingly complex and hard to define. I will look at it from 3 points of view:
- School Algebra
- Universal Algebra
- Category Theory Approach to Algebra
Ill take these in turn.
School Algebra
There is quite a lot to learn when we move from arithmetic to algebra. We learn about equations and what are the various symbols that make up an equation (More about equations on the page here). Along with this we learn about the use of 'variables' to represent unknowns, functions and binary operations, and so on.
Each side of an equation is an 'expression', which is recursively defined, so it can be built up to any level of complexity.
Then we have to learn the rules for manipulating these equations, this allows us to replace parts of an equation with something else that is equivalent. This allows us to work out things that weren't evident from the original form of the equations, perhaps find the value of a given variable.
There are certain rules that define the algebra and so they can't be derived from other rules. These rules, that are a given starting point, are known as axioms.
Universal Algebra
This is an attempt to generalise algebra so that it can be studied independently of any specific algebra, such as number algebra or matrix algebra.
We can divide it into syntax and semantics:
Syntax
The functions and operations in an algebra are often in a form like this:
f: Xn->X
So, for example, we may have an operation (say addition) that takes two operands and returns a single value. We might represent this like this:
X+X->X
This is known as 'infix' notation where the operation symbol is put between the values it is operating on. In order to generalise this to any number of operands, we will use prefix notation, this also emphasises that it is a function like this:
+(X,X)->X
We can represent (X,X) as X². So when we generalise from 'binary' to 'n-ary' operations we get the form here:
f: Xn->X
We can have multiple operations so we use capital sigma to indicate this:
Σ f: Xn->X
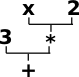 |
Using these function signatures we can build up expressions of any complexity. This is built up recursively, that is, an operand may be not only a constant of a variable but also another expression. The expression on the left would usually be written: 3+x*2 but I have drawn it at a tree structure to emphasise its recursive nature. |
So the syntax defines how expressions are built up, to define the result of calculation we need the semantics:
Semantics
To find the result of an operation we need to do the arithmetic or whatever the operation is. However there is a lot we can find out about about the result without actually doing the calculation. Algebras have a set of axioms and rules.
We often think of this as a sort of 'logic' layer over the algebra.
More about this on the page here.
Category Theory Approach to Algebra
The general approach in category theory is, not to understand something by building it up from its component parts, but to model its external properties. So we can find mappings between algebras that preserve their structure: linear transforms, group morphisms, etc.
There are two approches to working with algebras in category theory, ether,
- Based on monads
- Based on Lawvere theory
Lawvere Algebraic Theory
Bill Lawvere introduced a new categorical method for doing universal algebra. This defines an algebraic theory as:
- a category with finite products
- possessing a “generic algebra” (e.g., a generic group)
- then define a model of that theory (e.g., a group) as a product-preserving functor out of that category.
This is a category T with finite products.
Models of T are finite product preserving functors T-> Set.
Algebraic theories (left exact theories) are categories T with finite limits, whose models are finitely continuous functors T-> Set.
Monads
Algebras are related to monads and adjunctions. Each monad gives rise to a whole category of algebras.
An 'equational theory' is called a 'T-Algebra'. This gives rise to a free -| forgetful adjunction between sets and the category of models of the theory.
- forgetful functor U: T-Alg -> Sets
- free functor F: Sets -> T-Alg
More about category theory on the page here and specifically categorical algebra on the page here.
